
【题目】四张扑克牌的点数分别是2,3,4,8,将它们洗匀后背面朝上放在桌上.
(1)从中随机抽取一张牌,求这张牌的点数是偶数的概率;
(2)从中随机抽取一张牌,接着再抽取一张,求这两张牌的点数都是偶数的概率.
【答案】
(1)解:根据数字2,3,4,8中一共有3个偶数,
故从中随机抽取一张牌,这张牌的点数偶数的概率为: ![]()
(2)解:根据从中随机抽取一张牌,接着再抽取一张,列树状图如下:
![]()
根据树状图可知,一共有12种情况,两张牌的点数都是偶数的有6种,
故连续抽取两张牌的点数都是偶数的概率是: ![]() =
= ![]()
【解析】(1)利用数字2,3,4,8中一共有3个偶数,总数为4,即可得出点数偶数的概率;(2)利用树状图列举出所有情况,让点数都是偶数的情况数除以总情况数即为所求的概率.
【考点精析】关于本题考查的列表法与树状图法和概率公式,需要了解当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率;一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=m/n才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边长为2cm,∠A=60°. ![]() 是以点A为圆心、AB长为半径的弧,
是以点A为圆心、AB长为半径的弧, ![]() 是以点B为圆心、BC长为半径的弧.则阴影部分的面积为cm2 .
是以点B为圆心、BC长为半径的弧.则阴影部分的面积为cm2 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据悉,2013年财政部核定海南省发行的60亿地方政府“债券资金”,全部用于交通等重大项目建设.以下是60亿“债券资金”分配统计图: 
(1)请将条形统计图补充完整;
(2)在扇形统计图中,a= , b=(都精确到0.1);
(3)在扇形统计图中,“教育文化”对应的扇形圆心角的度数为°(精确到1°)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形纸片ABCD中,∠A=60°,将纸片折叠,点A、D分别落在点A′、D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时, ![]() 的值为( )
的值为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在梯形ABCD中,AD∥BC,AB=DC,对角线AC、BD交于点O,AC⊥BD,E、F、G、H分别是AB、BC、CD、DA的中点. 
(1)求证:四边形EFGH是正方形;
(2)若AD=2,BC=4,求四边形EFGH的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知梯形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3, 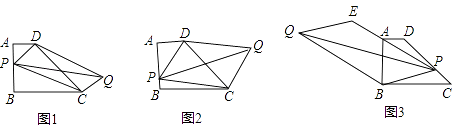
问题1:如图1,P为AB边上的一点,以PD,PC为边作平行四边形PCQD,请问对角线PQ,DC的长能否相等,为什么?
问题2:如图2,若P为AB边上一点,以PD,PC为边作平行四边形PCQD,请问对角线PQ的长是否存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.
问题3:若P为AB边上任意一点,延长PD到E,使DE=PD,再以PE,PC为边作平行四边形PCQE,请探究对角线PQ的长是否也存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.
问题4:如图3,若P为DC边上任意一点,延长PA到E,使AE=nPA(n为常数),以PE、PB为边作平行四边形PBQE,请探究对角线PQ的长是否也存在最小值?如果存在,请求出最小值,如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用一面墙(墙的长度不超过45m),用80m长的篱笆围一个矩形场地. 
(1)怎样围才能使矩形场地的面积为750m2?
(2)能否使所围矩形场地的面积为810m2 , 为什么?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com