
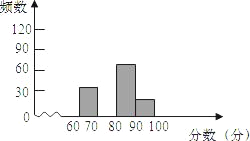
【题目】某校举行手工制作比赛,赛后整理参赛同学的成绩,并制作成图表如下:
分数段 | 频数 | 频率 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | m | 0.45 |
80≤x<90 | 60 | n |
90≤x<100 | 20 | 0.1 |
请根据以上图表提供的信息,解答下列问题:
(1)表中m和n所表示的数分别为:m=______,n=______,
(2)请在图中,补全频数分布直方图;
(3)比赛成绩的中位数落在哪个分数段?
(4)如果比赛成绩80分以上(含80分)可以获得奖励,那么获奖率是多少?
科目:初中数学 来源: 题型:
【题目】一个四边形被一条对角线分割成两个三角形,如果分割所得的两个三角形相似,我们就把这条对角线称为相似对角线.
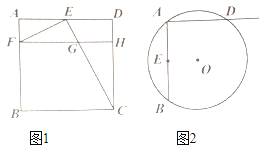
(1)如图,正方形![]() 的边长为4,
的边长为4,![]() 为
为![]() 的中点,点
的中点,点![]() ,
,![]() 分别在边
分别在边![]() 和
和![]() 上,且
上,且![]() ,线段
,线段![]() 与
与![]() 交于点
交于点![]() ,求证:
,求证:![]() 为四边形
为四边形![]() 的相似对角线;
的相似对角线;
(2)在四边形![]() 中,
中,![]() 是四边形
是四边形![]() 的相似对角线,
的相似对角线,![]() ,
,![]() ,
,![]() ,求
,求![]() 的长;
的长;
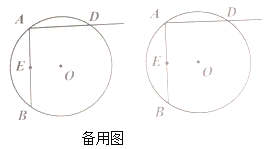
(3)如图,已知四边形![]() 是圆
是圆![]() 的内接四边形,
的内接四边形,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 是射线
是射线![]() 上的动点,若
上的动点,若![]() 是四边形
是四边形![]() 的相似对角线,请直接写出线段
的相似对角线,请直接写出线段![]() 的长度(写出3个即可).
的长度(写出3个即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c经过点(﹣1,0),对称轴为直线l,则下列结论:①abc>0;②a+b+c>0;③a+c>0;④a+b>0,正确的是( )

A. ①②④B. ②④C. ①③D. ①④
查看答案和解析>>
科目:初中数学 来源: 题型:
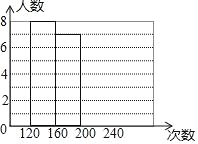
【题目】某体育老师随机抽取了九年级甲、乙两班部分学生进行一分钟跳绳的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
分组 | 频数 | 频率 |
第一组(0≤x<120) | 3 | 0.15 |
第二组(120≤x<160) | 8 | a |
第三组(160≤x<200) | 7 | 0.35 |
第四组(200≤x<240) | b | 0.1 |
(1)频数分布表中a=____,b=_____,并将统计图补充完整;
(2)如果该校九年级共有学生360人,估计跳绳能够一分钟完成160或160次以上的学生有多少人?
(3)已知第一组中有两个甲班学生,第四组中只有一个甲班学生,老师随机从这两个组中各选一名学生谈测试体会,则所选两人正好都是甲班学生的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A、B的坐标分别为![]() ,
,![]() ,点M是AO中点,
,点M是AO中点,![]() 的半径为2.
的半径为2.
![]() 若
若![]() 是直角三角形,则点P的坐标为______
是直角三角形,则点P的坐标为______![]() 直接写出结果
直接写出结果![]()
![]() 若
若![]() ,则BP与
,则BP与![]() 有怎样的位置关系?为什么?
有怎样的位置关系?为什么?
![]() 若点E的坐标为
若点E的坐标为![]() ,那么
,那么![]() 上是否存在一点P,使
上是否存在一点P,使![]() 最小,如果存在,求出这个最小值,如果不存在,简要说明理由.
最小,如果存在,求出这个最小值,如果不存在,简要说明理由.
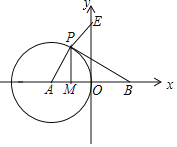
查看答案和解析>>
科目:初中数学 来源: 题型:
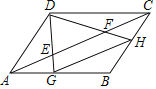
【题目】如图,E,F是平行四边形ABCD对角线AC上两点,AE=CF=![]() AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则
AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
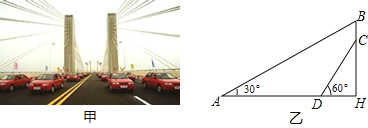
【题目】某大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米, ![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
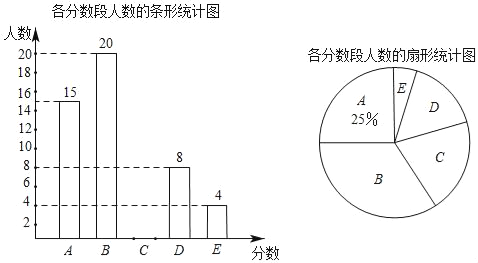
【题目】今年9月28日,某中学初三年级同学进行了中招体育模拟考试,王老师为了更加科学有效地制定后期训练计划,对本班同学的体考成绩进行了统计,并绘制了如图的条形统计图和扇形统计图,其中体育成绩共分为五个等级:A:46分﹣50分;B:41分﹣45分C:36分﹣40分;D:31分﹣35分;E:30分及以下,请根据图中所给的信息完成下列问题:
(1)将上面的条形统计图补充完整:并计算扇形统计图中E等级所对应的圆心角度数为 .
(2)该班A等级中共有5名同学获得满分,其中男同学只有2名,现从这5名同学中任选2名同学在班上进行经验交流,请用树状图或列表法求恰好选到一名男同学和一名女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
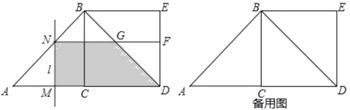
【题目】如图,△ABC中,∠ACB=90°,AC=CB=2,以BC为边向外作正方形BCDE,动点M从A点出发,以每秒1个单位的速度沿着A—C—D的路线向D点匀速运动(M不与A、D重合);过点M作直线l⊥AD,l与路线A—B—D相交于点N,设运动时间为t秒:
(1)当点M在AC上时,BN=_____.(用含t的代数式表示)
(2)过N作NF⊥ED,垂足为F,矩形MDFN与△ABD重叠部分的面积为S,求S的最大值
(3)当点M在CD上时(含点C),是否存在点M,使△DEN为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com