
【题目】阅读下面材料:
小天在学习锐角三角函数中遇到这样一个问题:在Rt△ABC中,∠C=90°,∠B=22.5°,则tan22.5°=
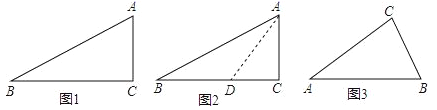
小天根据学习几何的经验,先画出了几何图形(如图1),他发现22.5°不是特殊角,但它是特殊角45°的一半,若构造有特殊角的直角三角形,则可能解决这个问题.于是小天尝试着在CB边上截取CD=CA,连接AD(如图2),通过构造有特殊角(45°)的直角三角形,经过推理和计算使问题得到解决.
请回答:tan22.5°= .
参考小天思考问题的方法,解决问题:
如图3,在等腰△ABC 中,AB=AC,∠A=30°,请借助△ABC,构造出15°的角,并求出该角的正切值.
【答案】(1)![]() ﹣1;
﹣1;![]() ﹣1;(2)2﹣
﹣1;(2)2﹣![]() .
.
【解析】
试题分析:如图2,设CD=CA=a,△ACD为等腰直角三角形,则AD=![]() a,易得∠DAB=∠B=22.5°,所以DB=DA=
a,易得∠DAB=∠B=22.5°,所以DB=DA=![]() a,再在Rt△ABC中,利用正切定义可计算出tanB=
a,再在Rt△ABC中,利用正切定义可计算出tanB=![]() ﹣1,即tan22.5°=
﹣1,即tan22.5°=![]() ﹣1;
﹣1;
如图3,延长BA到D,使AD=AB,则AB=AD=AC,则∠D=∠ACD,利用三角形外角性质易得∠D=15°,作CH⊥AB于H,设CH=x,利用含30度三边的关系得到AC=2x,AH=![]() x,则AD=AC=2x,DH=AD+AH=(2+
x,则AD=AC=2x,DH=AD+AH=(2+![]() )x,然后在Rt△DCH中,利用正切的定义可计算出tanD=2﹣
)x,然后在Rt△DCH中,利用正切的定义可计算出tanD=2﹣![]() ,即tan15°=2﹣
,即tan15°=2﹣![]() .
.
试题解析:如图2,设CD=CA=a,则AD=![]() a,
a,
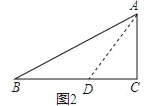
∵∠B=22.5°,∠ADC=45°,
∴∠DAB=22.5°,
∴∠DAB=∠B,
∴DB=DA=![]() a,
a,
∴BC=BD+CD=(![]() +1)a,
+1)a,
在Rt△ABC中,tanB=![]() ,
,
即tan22.5°=![]() ﹣1;
﹣1;
如图3,延长BA到D,使AD=AB,则AB=AD=AC,

∴∠D=∠ACD,
∵∠CAB=∠D+∠ACD=30°,
∴∠D=15°,
作CH⊥AB于H,设CH=x,则AC=2x,AH=![]() x,
x,
∴AD=AC=2x,
∴DH=AD+AH=(2+![]() )x,
)x,
在Rt△DCH中,tanD=![]() ,
,
即tan15°=2﹣![]() .
.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
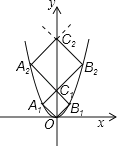
【题目】如图,已知点A1,A2,…,A2011在函数y=x2位于第二象限的图象上,点B1,B2,…,B2011在函数y=x2位于第一象限的图象上,点C1,C2,…,C2011在y轴的正半轴上,若四边形OA1C1B1、C1A2C2B2,…,C2010A2011C2011B2011都是正方形,则正方形C2010A2011C2011B2011的边长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某气球内充满一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.
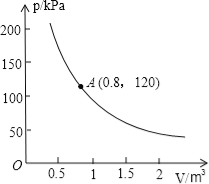
(1)写出这一函数的表达式.
(2)当气体体积为1 m3时,气压是多少?
(3)当气球内的气压大于140 kPa时,气球将爆炸,为了安全起见,气体的体积应不大于多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】保护水资源,人人有责,我国是缺水国家,目前可利用淡水资源总量仅约为899000亿立方米,899000亿用科学记数法表示为( )
A.8.99×1013 B.0.899×1014 C.8.99×1012 D.89.9×1011
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,反比例函数![]() 的图象过点A(1,6).
的图象过点A(1,6).
(1)求反比例函数的表达式;
(2)过点A的直线与反比例函数![]() 图象的另一个交点为B,与x轴交于点P,若AP=2PB,求点P的坐标.
图象的另一个交点为B,与x轴交于点P,若AP=2PB,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com