
【题目】已知![]() 中,记
中,记![]() ,
,![]() .
.
(1)如图![]() ,若
,若![]() 平分
平分![]() ,
,![]() 、
、![]() 分别是
分别是![]() 的外角
的外角![]() 和
和![]() 的平分线,
的平分线,![]() ,用含
,用含![]() 的代数式表示
的代数式表示![]() 的度数,用含
的度数,用含![]() 的代数式表示
的代数式表示![]() 的度数,并说明理由.
的度数,并说明理由.

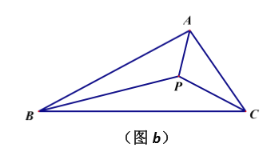
(2)如图![]() ,若点
,若点 ![]() 为
为![]() 的三条内角平分线的交点,
的三条内角平分线的交点,![]() 于点
于点 ![]() , 猜想(1)中的两个结论是否发生变化,补全图形并直接写出你的结论.
, 猜想(1)中的两个结论是否发生变化,补全图形并直接写出你的结论.
![]() .
.
![]() .
.
科目:初中数学 来源: 题型:
【题目】用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,求三角形各边的长;
(2)能围成有一边的长是4cm的等腰三角形吗?若能,求出其他两边的长;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
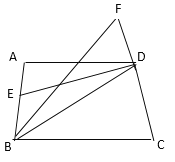
【题目】如图,四边形ABCD中,AD∥BC,DE平分∠ADB,∠BDC=∠BCD,
(1)求证:∠1+∠2=90°.
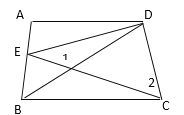
(2)若∠ABD的平分线与CD的延长线交于F,且∠F=55°,求∠ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
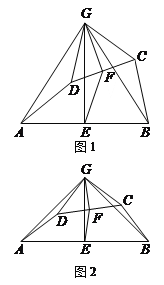
【题目】如图1,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC.
(1)求证:AD=BC;
(2)求证:△AGD∽△EGF;
(3)如图2,若AD、BC所在直线互相垂直,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=![]() BD
BD
其中正确结论的为______(请将所有正确的序号都填上).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O.
(1)求证:△AEC≌△BED;
(2)若∠1=40°,求∠BDE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
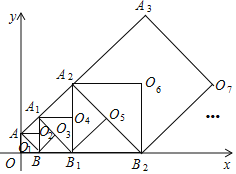
【题目】如图,正方形AOBO2的顶点A的坐标为A(0,2),O1为正方形AOBO2的中心;以正方形AOBO2的对角线AB为边,在AB的右侧作正方形ABO3A1,O2为正方形ABO3A1的中心;再以正方形ABO3A1的对角线A1B为边,在A1B的右侧作正方形A1BB1O4,O3为正方形A1BB1O4的中心;再以正方形A1BB1O4的对角线A1B1为边在A1B1的右侧作正方形A1B1O5A2,O4为正方形A1B1O5A2的中心:…;按照此规律继续下去,则点O2018的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
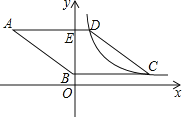
【题目】如图,菱形ABCD的边AD⊥y轴,垂足为点E,顶点A在第二象限,顶点B在y轴的正半轴上,反比例函数y=![]() (k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE,则k的值为( )
(k≠0,x>0)的图象同时经过顶点C,D.若点C的横坐标为5,BE=3DE,则k的值为( )
A. ![]() B. 3 C.
B. 3 C. ![]() D. 5
D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列材料,然后解决后面的问题.
材料:一个三位数![]() (百位数为a,十位数为b,个位数为c),若a+c=b,则称这个三整数
(百位数为a,十位数为b,个位数为c),若a+c=b,则称这个三整数![]() 为“协和数”,同时规定c=
为“协和数”,同时规定c=![]() (k≠0),k称为“协和系数”,如264,因为它的百位上数字2与个位数字4之和等于十位上的数字6,所有264是“协和数”,则“协和数”k=2×4=8.
(k≠0),k称为“协和系数”,如264,因为它的百位上数字2与个位数字4之和等于十位上的数字6,所有264是“协和数”,则“协和数”k=2×4=8.
(1)对于“协和数”![]() ,求证:“协和数”
,求证:“协和数”![]() 能被11整除.
能被11整除.
(2)已知有两个十位数相同的“协和数”![]() ,
,![]() (a1>a2),且k1﹣k2=1,若y=k1+k2,用含b的式子表示y.
(a1>a2),且k1﹣k2=1,若y=k1+k2,用含b的式子表示y.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com