
在菱形ABCD和正三角形BGF中,∠ABC=60°,P是DF的中点,连接PG、PC.
(1)如图1,当点G在BC边上时,易证:PG=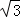 PC.(不必证明)
PC.(不必证明)
(2)如图2,当点F在AB的延长线上时,线段PC、PG有怎样的数量关系,写出你的猜想,并给与证明;
(3)如图3,当点F在CB的延长线上时,线段PC、PG又有怎样的数量关系,写出你的猜想(不必证明).
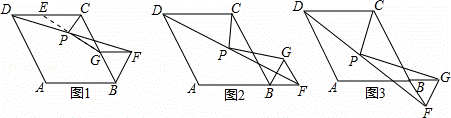
(1)提示:如图1:延长GP交DC于点E,
利用△PED≌△PGF,得出PE=PG,DE=FG,
∴CE=CG,
∴CP是EG的中垂线,
在RT△CPG中,∠PCG=60°,
∴PG= PC.
PC.
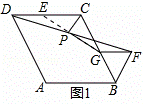
(2)如图2,延长GP交DA于点E,连接EC,GC,
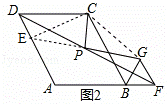
∵∠ABC=60°,△BGF正三角形
∴GF∥BC∥AD,
∴∠EDP=∠GFP,
在△DPE和△FPG中

∴△DPE≌△FPG(ASA)
∴PE=PG,DE=FG=BG,
∵∠CDE=CBG=60°,CD=CB,
在△CDE和△CBG中,

∴△CDE≌△CBG(SAS)
∴CE=CG,∠DCE=∠BCG,
∴∠ECG=∠DCB=120°,
∵PE=PG,
∴CP⊥PG,∠PCG=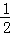 ∠ECG=60°
∠ECG=60°
∴PG=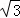 PC.
PC.
(3)猜想:PG=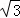 PC.
PC.
证明:如图3,延长GP到H,使PH=PG,连接CH,CG,DH,作ME∥DC
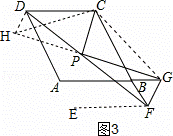
∵P是线段DF的中点,
∴FP=DP,
∵∠GPF=∠HPD,
∴△GFP≌△HDP,
∴GF=HD,∠GFP=∠HDP,
∵∠GFP+∠PFE=120°,∠PFE=∠PDC,
∴∠CDH=∠HDP+∠PDC=120°,
∵四边形ABCD是菱形,
∴CD=CB,∠ADC=∠ABC=60°,点A、B、G又在一条直线上,
∴∠GBC=120°,
∵四边形BEFG是菱形,
∴GF=GB,
∴HD=GB,
∴△HDC≌△GBC,
∴CH=CG,∠DCH=∠BCG,
∴∠DCH+∠HCB=∠BCG+∠HCB=120°,
即∠HCG=120°
∵CH=CG,PH=PG,
∴PG⊥PC,∠GCP=∠HCP=60°,
∴PG=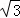 PC.
PC.


 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:
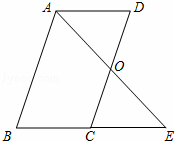
已知:如图,▱ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)求证:△AOD≌△EOC;
(2)连接AC,DE,当∠B=∠AEB= °时,四边形ACED是正方形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).
(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;
(3)△A2B2C2的面积是 平方单位.

查看答案和解析>>
科目:初中数学 来源: 题型:
某小7名初中男生参加引体向上体育测试的成绩分别为:8,5,7,5,8,6,8,则这组数据的众数和中位数分别为( )
|
| A. | 6,7 | B. | 8,7 | C. | 8,6 | D. | 5,7 |
查看答案和解析>>
科目:初中数学 来源: 题型:
苹果的单价为a元/千克,香蕉的单价为b元/千克,买2千克苹果和3千克香蕉共需( )
|
| A. | (a+b)元 | B. | (3a+2b)元 | C. | (2a+3b)元 | D. | 5(a+b)元 |
查看答案和解析>>
科目:初中数学 来源: 题型:
某文具厂计划加工3000套画图工具,为了尽快完成任务,实际每天加工画图工具的数量是原计划的1.2倍,结果提前4天完成任务,求该文具厂原计划每天加工这种画图工具的数量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com