
【题目】如图,已知D是△ABC中一边BC上的中点 ,AC∥BE,连接ED并延长ED交AC于点N,作DM⊥EN于点D交AB于点M.
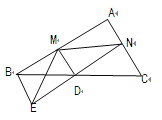
(1)求证:BE=CN
(2)试判断BM+CN与MN的大小关系,并说明理由.
【答案】(1)证明见解析;(2)BM+CN>MN.
【解析】
试题分析:(1)根据平行线的性质可证∠C=∠DBE,根据中点的定义可证BD=CD,根据AAS可证△BDE≌△CDN,根据全等三角形的性质可证DE=DN,BE=CN;
(2)根据DM⊥EN,可得∠MDE=∠MDN=90°,因为DE=DN,根据中垂线的性质可证ME=MN,根据三角形三边的关系可证BM+BE>ME,所以可证
试题解析:(1)∵AC//BE,BM+CN>MN.
∴∠C=∠DBE,
∵D是BC中点,
∴BD=CD,
又∠BDE=∠CDN,
∴△BDE≌△CDN(AAS),
∴DE=DN,BE=CN,
(2)∵DM⊥EN,
∴∠MDE=∠MDN=90°,
∵DE=DN,
∴ME=MN,
在△BME中BM+BE>ME,
又BE=CN,ME=MN,
∴BM+CN>MN.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D为BC边的中点,以点D为顶点的∠EDF的两边分别与边AB,AC交于点E,F,且∠EDF与∠A互补.
(1)如图1,若AB=AC,且∠A=90°,则线段DE与DF有何数量关系?请直接写出结论;
(2)如图2,若AB=AC,那么(1)中的结论是否还成立?若成立,请给出证明;若不成立,请说明理由;
(3)如图3,若AB:AC=m:n,探索线段DE与DF的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E.∠ADC =70°.

(1)求∠EDC的度数;
(2)若∠ABC =n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移, 使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示),不改变,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,破残的圆形轮片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D.
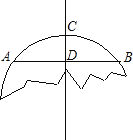
①求作此残片所在的圆O(不写作法,保留作图痕迹);
②已知:AB=12cm,直径为20cm,求①中CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解一元二次方程x2+4x﹣5=0,此方程可变形为( )
A.(x+2)2=9
B.(x﹣2)2=9
C.(x+2)2=1
D.(x﹣2)2=1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,D、E分别是AB、AC的中点,过点E作EF∥AB,交BC于点F.
(1)求证:四边形DBFE是平行四边形;
(2)当△ABC满足什么条件时,四边形DBFE是菱形?为什么?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com