
| A. | 4$\sqrt{3}$-3$\sqrt{3}$=1 | B. | $\sqrt{2}$$+\sqrt{3}$=$\sqrt{5}$ | C. | $\frac{\sqrt{8}}{\sqrt{2}}$=2 | D. | $\sqrt{(-3)^{2}}$=-3 |
分析 根据二次根式的加减法则对各选项进行逐一分析即可.
解答 解:A、4$\sqrt{3}$-3$\sqrt{3}$=$\sqrt{3}$≠1,故本选项错误;
B、$\sqrt{2}$与$\sqrt{3}$不是同类项,不能合并,故本选项错误;
C、$\frac{\sqrt{8}}{\sqrt{2}}$=$\frac{2\sqrt{2}}{\sqrt{2}}$=2,故本选项正确;
D、$\sqrt{(-3)^{2}}$=3≠-3,故本选项错误.
故选C.
点评 本题考查的是二次根式的加减法,熟知二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变是解答此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
| 序号项目 | 1 | 2 | 3 | 4 | 5 |
| 笔试成绩/分 | 85 | 84 | 84 | 90 | 80 |
| 面试成绩/分 | 90 | 86 | 80 | 90 | 85 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
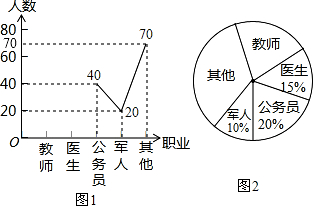
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
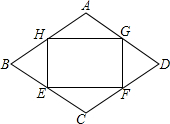 如图,菱形ABCD中,∠B=60°,AB=4cm,E、F、G、H分别是菱形四边中点,则四边形EFGH的面积为4$\sqrt{3}$cm2.
如图,菱形ABCD中,∠B=60°,AB=4cm,E、F、G、H分别是菱形四边中点,则四边形EFGH的面积为4$\sqrt{3}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
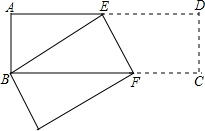 如图,在长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )
如图,在长方形ABCD中,AB=3cm,AD=9cm,将此长方形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为( )| A. | 6cm2 | B. | 8cm2 | C. | 10cm2 | D. | 12cm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com