
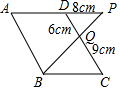
 图中,ABCD为平行四边形,ADP、BQP及CQD均为直线.
图中,ABCD为平行四边形,ADP、BQP及CQD均为直线.分析 (1)由四边形ABCD是平行四边形知AP∥BC,据此得出∠QBC=∠QPD、∠QCB=∠QDP,即可证得△BCQ∽△PDQ;
(2)根据相似三角形的性质得出$\frac{BC}{PD}$=$\frac{CQ}{DQ}$即$\frac{BC}{8}$=$\frac{9}{6}$,求得BC的长,由周长公式求解可得.
解答 解:(1)∵四边形ABCD是平行四边形,
∴AP∥BC,
∴∠QBC=∠QPD、∠QCB=∠QDP,
∴△BCQ∽△PDQ;
(2)∵△BCQ∽△PDQ,
∴$\frac{BC}{PD}$=$\frac{CQ}{DQ}$,即$\frac{BC}{8}$=$\frac{9}{6}$,
解得:BC=12,
则四边形ABCD的周长为2(12+6+9)=54cm.
点评 本题主要考查相似三角形的判定与性质、平行四边形的性质,熟练掌握相似三角形的判定与性质是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | 2 018 | B. | 2 008 | C. | 2 014 | D. | 2 012 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是9cm,内壁高12cm,则这只铅笔的长度可能是( )
如图,一支铅笔放在圆柱体笔筒中,笔筒的内部底面直径是9cm,内壁高12cm,则这只铅笔的长度可能是( )| A. | 9cm | B. | 12cm | C. | 15cm | D. | 18cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com