
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,且
,且![]() .直线
.直线![]() 与抛物线交于
与抛物线交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线的顶点,设直线
是抛物线的顶点,设直线![]() 上方的抛物线上的动点
上方的抛物线上的动点![]() 的横坐标为
的横坐标为![]() .
.
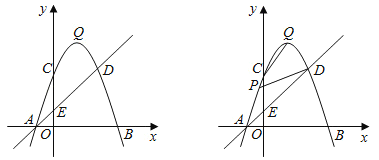
(1)求该抛物线的解析式及顶点![]() 的坐标.
的坐标.
(2)连接![]() ,直接写出线段
,直接写出线段![]() 与线段
与线段![]() 的数量关系和位置关系.
的数量关系和位置关系.
(3)连接![]() ,当
,当![]() 为何值时
为何值时![]() ?
?
(4)在直线![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 为等腰直角三角形?若存在,请直接写出点
为等腰直角三角形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ,点
,点![]() 的坐标为
的坐标为![]() (2)线段
(2)线段![]() 与线段
与线段![]() 平行且相等(3)
平行且相等(3)![]() 或1(4)存在;点
或1(4)存在;点![]() 的坐标为(0,3)或(
的坐标为(0,3)或(![]() ,2)
,2)
【解析】
(1)直线y=x+1与抛物线交于A点,可得点A和点E坐标,则点B、C的坐标分别为:(3,0)、(0,3),即可求解;
(2)CQ=![]() =AE,直线AQ和AE的倾斜角均为45°,即可求解;
=AE,直线AQ和AE的倾斜角均为45°,即可求解;
(3)根据题意将△APD的面积和![]() △DAB的面积表示出来,令其相等,即可解出m的值;
△DAB的面积表示出来,令其相等,即可解出m的值;
(4)分∠QOH=90°、∠PQH=90°、∠QHP=90°三种情况,分别求解即可.
解:(1)直线![]() 与抛物线交于
与抛物线交于![]() 点,则点
点,则点![]() 、点
、点![]() .
.
∵![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,
,
故抛物线的表达式为![]() ,
,
将点![]() 的坐标代入,得
的坐标代入,得![]() ,解得
,解得![]() ,
,
故抛物线的表达式为![]() ,
,
函数的对称轴为![]() ,故点
,故点![]() 的坐标为
的坐标为![]() .
.
(2)CQ=AE,且CQ∥AE,
理由是:![]() ,
,
![]() ,
,
∴CQ=AE,
直线CQ表达式中的k=![]() =1,与直线AE表达式中k相等,故AE∥CQ,
=1,与直线AE表达式中k相等,故AE∥CQ,
故线段CQ与线段AE的数量关系和位置关系是平行且相等;
(3)联立直线![]() 与抛物线的表达式,并解得
与抛物线的表达式,并解得![]() 或2.故点
或2.故点![]() .
.
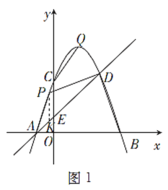
如图1,过点![]() 作
作![]() 轴的平行线,交
轴的平行线,交![]() 于点
于点![]() ,
,
设点![]() ,则点
,则点![]() .
.
![]()
![]()
![]()
![]()
解得![]() 或1.
或1.
(4)存在,理由:
设点![]() ,点
,点![]() ,
,![]() ,而点
,而点![]() ,
,
①当![]() 时,如图2,
时,如图2,
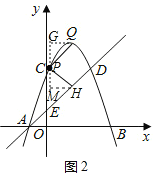
过点![]() 作
作![]() 轴的平行线,分别交过点
轴的平行线,分别交过点![]() 、点
、点![]() 与
与![]() 轴的平行线于点
轴的平行线于点![]() 、
、![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
在△PGQ和△HMP中,
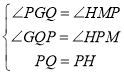 ,
,
![]() ,
,
![]() ,
,![]() ,
,
即:![]() ,
,![]() ,
,
解得m=2或n=3,
当n=3时,![]()
解得:![]() 或2(舍去),
或2(舍去),
故点P![]() ;
;
②当![]() 时,如图3,
时,如图3,
![]() ,则点
,则点![]() 、
、![]() 关于抛物线对称轴对称,即
关于抛物线对称轴对称,即![]() 垂直于抛物线的对称轴,
垂直于抛物线的对称轴,
而对称轴与![]() 轴垂直,故
轴垂直,故![]() 轴,则
轴,则![]() ,
,

可得:△MQP和△NQH都是等腰直角三角形,
MQ=MP,
∵MQ=1-m,MP=4-n,
∴n=3+m,代入![]() ,
,
解得:![]() 或1(舍去),
或1(舍去),
故点P![]() ;
;
③当![]() 时,
时,
如图4所示,点![]() 在
在![]() 下方,与题意不符,故舍去.
下方,与题意不符,故舍去.
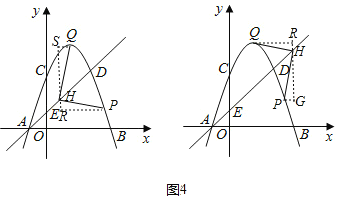
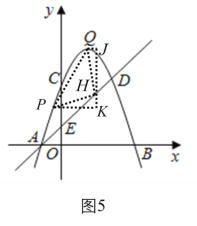
如图5,P在y轴右侧,同理可得△PHK≌△HQJ,
可得QJ= HK,
∵QJ=t-1,HK=t+1-n,
∴t-1=t+1-n,
∴n=2,
∴![]() ,
,
解得:m=![]() (舍去)或
(舍去)或![]() ,
,
∴点P(![]() ,2)
,2)
综上,点![]() 的坐标为:
的坐标为:![]() 或(
或(![]() ,2)
,2)


科目:初中数学 来源: 题型:
【题目】为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.
(1)八(1)班抽中歌曲《我和我的祖国》的概率是__________;
(2)试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
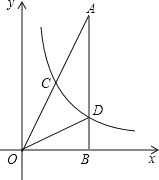
【题目】如图,在△AOB中,∠ABO=90°,OB=4,AB=8,反比例函数y=![]() 在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.
在第一象限内的图象分别交OA,AB于点C和点D,且△BOD的面积S△BOD=4.
(1)求反比例函数解析式;
(2)求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
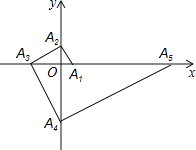
【题目】如图,点A1的坐标为(1,0),A2在y轴的正半轴上,且∠A1A2O=30°,过点A2作A2A3⊥A1A2,垂足为A2,交x轴于点A3;过点A3作A3A4⊥A2A3,垂足为A3,交y轴于点A4;过点A4作A4A5⊥A3A4,垂足为A4,交x轴于点A5;过点A5作A5A6⊥A4A5,垂足为A5,交y轴于点A6;…按此规律进行下去,则点A2016的纵坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班甲、乙两名同学在5次引体向上测试中的有效次数如下:
甲:8,8,7,8,9.乙:5,9,7,10,9.
甲、乙两同学引体向上的平均数、众数、中位数、方差如下:
平均数 | 众数 | 中位数 | 方差 | |
甲 | 8 |
| 8 | 0.4 |
乙 |
| 9 |
| 3.2 |
根据以上信息,回答下列问题:
(1)表格中![]() _______,
_______,![]() _______,
_______,![]() _______.(填数值)
_______.(填数值)
(2)体育老师根据这5次的成绩,决定选择甲同学代表班级参加年级引体向上比赛,选择甲的理由是_______________________________________.班主任李老师根据去年比赛的成绩(至少9次才能获奖),决定选择乙同学代表班级参加年级引体向上比赛,选择乙的理由是_______________________________________.
(3)乙同学再做一次引体向上,次数为n,若乙同学6次引体向上成绩的中位数不变,请写出n的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)学校组织学生参加综合实践活动,他们参与了某种品牌运动鞋的销售工作,已知该运动鞋每双的进价为120元,为寻求合适的销售价格进行了4天的试销,试销情况如下表所示:
第1天 | 第2天 | 第3天 | 第4天 | |
售价x(元/双) | 150 | 200 | 250 | 300 |
销售量y(双) | 40 | 30 | 24 | 20 |
(1)观察表中数据,x,y满足什么函数关系?请求出这个函数关系式;
(2)若商场计划每天的销售利润为3000元,则其单价定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,对角线AC为⊙O的直径,过点C作AC的垂线交AD的延长线于点E,点F为CE的中点,连接DB,DC,DF.

(1)求∠CDE的度数;
(2)求证:DF是⊙O的切线;
(3)若AC=2![]() DE,求tan∠ABD的值.
DE,求tan∠ABD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,⊙O交x轴于A、B两点,直线FA⊥x轴于点A,点D在FA上,且DO平行于⊙O的弦MB,连接DM并延长交x轴于点C.
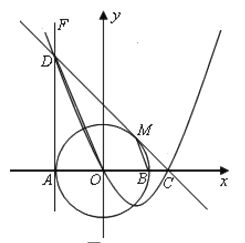
(1)判断直线DC与⊙O的位置关系,并给出证明;
(2)设点D的坐标为(-2,4),试求经过D、O、C三点的抛物线的解析式.
(3)若坐标平面内的点P,使得以点P和三点D、O、C为顶点的四边形是平行四边形,求P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
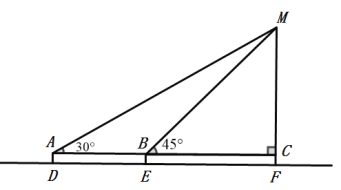
【题目】某校九年级数学兴趣小组的学生进行社会实践活动时,想利用所学的解直角三角形的知识测量教学楼的高度,他们先在点D处用测角仪测得楼顶M的仰角为30°,再沿DF方向前行40米到达点E处,在点E处测得楼顶M的仰角为45°,已知测角仪的高AD为1.5米,请根据他们的测量数据求此楼MF的高(结果精确到0.1m,参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com