
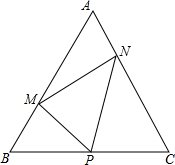
 等边△ABC,P为BC中点,∠MPN=60°,求证:△BPM∽△CNP∽△PNM;MP平分∠BMN;NP平分∠CNM;MN=BM+CN-$\frac{1}{2}$AB;BM•CN=$\frac{1}{4}$AB2.
等边△ABC,P为BC中点,∠MPN=60°,求证:△BPM∽△CNP∽△PNM;MP平分∠BMN;NP平分∠CNM;MN=BM+CN-$\frac{1}{2}$AB;BM•CN=$\frac{1}{4}$AB2. 分析 首先证明△BMP∽△CPN,推出$\frac{PM}{PN}$=$\frac{BM}{PC}$=$\frac{PB}{CN}$,由PB=PC,得到$\frac{PM}{BM}$=$\frac{PN}{BP}$,由此可证△BPM∽△CNP∽△PNM;根据相似三角形对应角相等,可以判断MP平分∠BMN;NP平分∠CNM;如图2中,作PE⊥MN于E,PF⊥AC于F,PG⊥AB于G,由△PMG≌△PME,推出MG=ME,再根据MN=ME+EN=MG+NF=BM-BG+CN-CF=BM+CN-BG-CF,即可证明MN=BM+CN-$\frac{1}{2}$AB,由△BMP∽△CPN,推出$\frac{BM}{PC}$=$\frac{PB}{CN}$,即可证明BM•CN=$\frac{1}{4}$AB2.
解答 证明:如图1中,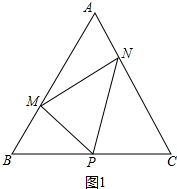 ∵△ABC是等边三角形,
∵△ABC是等边三角形,
∴AB=BC=AC,∠A=∠B=∠C=60°,
∵∠MPN=60°,∠MPC=∠B+∠PMB=∠MPN+∠NPC,
∴∠PMB=∠NPC,∵∠B=∠C,
∴△BMP∽△CPN,
∴$\frac{PM}{PN}$=$\frac{BM}{PC}$=$\frac{PB}{CN}$,
∵PB=PC,
∴$\frac{PM}{BM}$=$\frac{PN}{BP}$,∵∠B=∠MPN=60°,
∴△BMP∽△PMN∽△CPN.
∴∠BMP=∠PMN,∠MNP=∠CNP,
∴MP平分∠BMN;NP平分∠CNM.
如图2中,作PE⊥MN于E,PF⊥AC于F,PG⊥AB于G.
∵MP平分∠BMN;NP平分∠CNM,
∴PG=PE=PF,
在Rt△PMG和Rt△PME中,
$\left\{\begin{array}{l}{PM=PM}\\{PG=PE}\end{array}\right.$,
∴△PMG≌△PME,
∴MG=ME,同理可证NE=NF,
∴MN=ME+EN=MG+NF=BM-BG+CN-CF=BM+CN-BG-CF,
在Rt△PBG中,∵∠B=60°,∠PGB=90°,
∴∠BPG=30°,
∴BG=$\frac{1}{2}$PB=$\frac{1}{4}$BC=$\frac{1}{4}$AB,同理可证CF=$\frac{1}{4}$AB,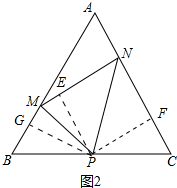
∴MN=BM+CN-$\frac{1}{4}$AB-$\frac{1}{4}$AB=BM+CN-$\frac{1}{2}$AB.
∵△BMP∽△CPN,
∴$\frac{BM}{PC}$=$\frac{PB}{CN}$,
∴BM•CN=PC•PB=$\frac{1}{2}$•BC•$\frac{1}{2}$•CB=$\frac{1}{4}$BC2=$\frac{1}{4}$AB2.
点评 本题考查三角形综合题、相似三角形的判定和性质、全等三角形的判定和性质、角平分线的性质等知识,解题的关键是熟练掌握相似三角形的判定方法,学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 下面的长方体是由A,B,C,D四个选项中所示的四个几何体拼接而成的,而且这四个几何体都是由4个同样大小的正方体组成的,那么长方体中,第四部分所对应的几何体应是( )
下面的长方体是由A,B,C,D四个选项中所示的四个几何体拼接而成的,而且这四个几何体都是由4个同样大小的正方体组成的,那么长方体中,第四部分所对应的几何体应是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 青岛国际帆船中心要修建一处公共服务设施,使它到三所运动员公寓A、B、C的距离相等.(不写作法,但要保留作图痕迹)
青岛国际帆船中心要修建一处公共服务设施,使它到三所运动员公寓A、B、C的距离相等.(不写作法,但要保留作图痕迹)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知如图,AD∥CF∥EB,AB=3,AC=5,DF=9,DA=2,CF=8,则,DE=$\frac{27}{5}$,EF=$\frac{18}{5}$,BE=4.
已知如图,AD∥CF∥EB,AB=3,AC=5,DF=9,DA=2,CF=8,则,DE=$\frac{27}{5}$,EF=$\frac{18}{5}$,BE=4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com