
����Ŀ����ͼ���ھ���OABC�У�AO=10��AB=8����ֱ��CD�۵�����OABC��һ��BC��ʹ��B����OA���ϵĵ�E�����ֱ���OC��OA���ڵ�ֱ��Ϊx�ᣬy�Ὠ��ƽ��ֱ������ϵ��������y=ax2+bx+c����O��D��C����.
��1����AD�ij��������ߵĽ���ʽ��
��2��һ����P�ӵ�E��������EC��ÿ��2����λ�����ٶ����C�˶���ͬʱ����Q�ӵ�C��������CO��ÿ��1����λ�����ٶ����O�˶�������P�˶�����Cʱ������ͬʱֹͣ�˶������˶�ʱ��Ϊt�룬��tΪ��ֵʱ����P��Q��CΪ�������������ADE���ƣ�
��3����N�������߶Գ����ϣ���M���������ϣ��Ƿ���������ĵ�M���N��ʹ��M��N��C��EΪ������ı�����ƽ���ı��Σ������ڣ���ֱ��д����M���N�����꣨��д�����̣����������ڣ���˵������.
���𰸡�
��1��
�⣺���ı���ABCOΪ���Σ�
���OAB=��AOC=��B=90�㣬AB=CO=8��AO=BC=10��
�����⣬�á�BDC�ա�EDC��
���B=��DEC=90�㣬EC=BC=10��ED=BD��
�ɹ��ɶ�����EO=6��
��AE=10��6=4��
��AD=x����BD=ED=8��x���ɹ��ɶ�������x2+42=��8��x��2����ã�x=3����AD=3��
��������y=ax2+bx+c����D��3��10����C��8��0����O��0,0,��
��  ���
���  �������ߵĽ���ʽΪ��y=
�������ߵĽ���ʽΪ��y= ![]() x2+
x2+ ![]() x��
x��
��2��
�ߡ�DEA+��OEC=90�㣬��OCE+��OEC=90�㣬
���DEA=��OCE��
�ɣ�1���ɵ�AD=3��AE=4��DE=5��
��CQ=t��EP=2t����PC=10��2t��
����PQC=��DAE=90�㣬��ADE�ס�QPC�� �� ![]() ����
���� ![]() �� ���t=
�� ���t= ![]() �� ����QPC=��DAE=90�㣬��ADE�ס�PQC�� ��
�� ����QPC=��DAE=90�㣬��ADE�ס�PQC�� �� ![]() ����
���� ![]() �� ���t=
�� ���t= ![]() �� �൱t=
�� �൱t= ![]() ��
�� ![]() ʱ����P��Q��CΪ��������������ADE���ƣ�
ʱ����P��Q��CΪ��������������ADE���ƣ�
��3��
�⣺������ڷ���������M��N�㣬������������ۣ���ECΪƽ���ı��εĶԽ��ߣ����������ߵĶԳ��ᾭ��EC�е㣬���ı���MENC��ƽ���ı��Σ���ôM���Ϊ�����߶��㣻 ��M��4�� ![]() ������ƽ���ı��εĶԽ�����ƽ�֣���ô�߶�MN�ر�EC�е㣨4��3��ƽ�֣���N��4��
������ƽ���ı��εĶԽ�����ƽ�֣���ô�߶�MN�ر�EC�е㣨4��3��ƽ�֣���N��4�� ![]() ���� ��ECΪƽ���ı��εıߣ���EC//MN��EC =MN����N��4��m������M��4��8��m+6����M��4+8��m��6���� ��M����4��m+6�����������ߵĽ���ʽ�У��ã�m=��38����ʱ N��4����38����
���� ��ECΪƽ���ı��εıߣ���EC//MN��EC =MN����N��4��m������M��4��8��m+6����M��4+8��m��6���� ��M����4��m+6�����������ߵĽ���ʽ�У��ã�m=��38����ʱ N��4����38����
M����4����32����
��M��12��m��6�����������ߵĽ���ʽ�У��ã�m=��26����ʱ N��4����26����M��12����32����
���ϣ����ڷ���������M��N�㣬�����ǵ�����Ϊ�� ��M1����4����32����N1��4����38�� ��M2��12����32����N2��4����26�� ��M3��4�� ![]() ����N3��4��
����N3��4�� ![]() ����
����
����������1�������۵����ʵ�EC=BC���Ӷ��ɽ��OE����AD=x����ED=8-x���ɹ��ɶ����ɵ�AD2+AE2=ED2 �� ���췽�̽��x��ֵ���Ӷ��ɵ�D�����꣬��D�����꣬C�����꣬O��������������߿��������2������á�DEA=��OCE���ɣ�1���ɵ�AD=3��AE=4��DE=5������CQ=t��EP=2t����PC=10��2t���������ۣ�����PQC=��DAE=90�㣬��ADE�ס�QPC���뵱��QPC=��DAE=90�㣬��ADE�ס�PQC���ֱ�д���ߵĹ�ϵ�������t����3���������ۣ���ECΪƽ���ı��εĶԽ��ߣ����������ߵĶԳ��ᾭ��EC�е㣬���ı���MENC��ƽ���ı��Σ���ôM���Ϊ�����߶��㣻�Ӷ��������M�����ꣻ��ECΪƽ���ı��εıߣ���EC//MN��EC =MN����N��4��m��������E��C��ƽ�ƹ�ϵ��M��N��ƽ�ƹ�ϵ��ͬ���ɵ�M��4��8��m+6����M��4+8��m��6��������M���������߽���ʽ���Ӷ����m��ֵ.
�����㾫����������Ҫ�����˶��κ�����ͼ��Ͷ��κ��������ʵ����֪ʶ�㣬��Ҫ���ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С������ȷ�����⣮


 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д� �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��PA��PB�ǡ�O�����ߣ�A��B���е㣬��C���ӻ�AB�ϵ�һ�����㣬����P=40�㣬���ACB�Ķ����ǣ�������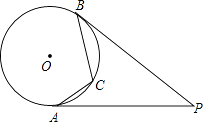
A.80��
B.110��
C.120��
D.140��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ�������������У�������Ϊ�ж���ABD�ա�BAC�������ǣ� )

A. ��D����C����BAD����ABC B. ��BAD����ABC����ABD����BAC
C. BD��AC����BAD����ABC D. AD��BC��BD��AC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���з��̽�Ӧ���⣺

��Ԫ���ż��ڼ䣬С�š�С����ͬѧ����ҳ�һ�����棬�����ǹ�����ƱʱС�źͰְֵĶԻ���

![]()

�����ͼ�е���Ϣ������⣺
��1��������һ���г����˶����ˣ�ѧ�������ˣ�
��2���������С����һ�㣬�����ַ�ʽ��Ʊ��ʡǮ��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�У���BCA=90�㣬CD�DZ�AB�ϵ����ߣ��ֱ����C��D��BA��BC��ƽ���߽��ڵ�E����DE��AC�ڵ�O������AE.
��1����֤���ı���ADCE�����Σ�
��2����AC=2DE����sin��CDB��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
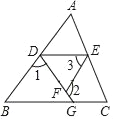
����Ŀ����ͼ����֪����3����B����1+��2��180�㣬��AED����C��С�������˵�����ɣ�
�������ղ�����������
�⣺��Ϊ��1+��2��180�㣨��֪��
����Ϊ��2+���� ����180�㣨�ڲ��ǵ����壩
���ԡ�1������ ������ ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����D�ڡ�ABC�ı�AB�ϣ��ҡ�ACD����A��
��1������BDC��ƽ����DE����BC�ڵ�E����Ҫ�߹���ͼ��������ͼ�ۼ���������д����������
��2���ڣ�1���������£���֤��DE��AC��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABP�ǵ��������Σ�AB=BP����ABΪֱ���ġ�O��AP�ڵ�D����BP�ڵ�C������BD��AC�ڵ�G��ֱ��MN����A���ҡ�PAM= ![]() ��ABP��
��ABP��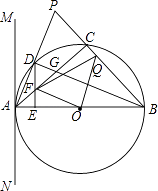
��1����˵��ֱ��MN�ǡ�O�����ߣ�
��2����D��DE��AB��E����AC��F����֤����DFG�ǵ��������Σ�
��3������FO������O��OQ��FO��BP�ڵ�Q������FQ����֤��FQ2=AF2+BQ2 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y= ![]() x��
x�� ![]() �����ABCO�ı�OC��BC�ֱ��ڵ�E��F����֪OA=3��OC=4�����CEF������ǣ�������
�����ABCO�ı�OC��BC�ֱ��ڵ�E��F����֪OA=3��OC=4�����CEF������ǣ�������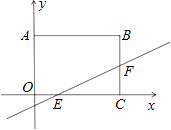
A.6
B.3
C.12
D.![]()
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com