
【题目】如图,已知一次函数![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,一次函数
,一次函数![]() 经过点
经过点![]() 与
与![]() 轴交于点.
轴交于点.
(1)求直线![]() 的解析式;
的解析式;
(2)点![]() 为
为![]() 轴上方直线
轴上方直线![]() 上一点,点
上一点,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 的中点,连接
的中点,连接![]() ,取
,取![]() 的中点
的中点![]() ,射线
,射线![]() 交
交![]() 轴于点
轴于点![]() ,点
,点![]() 为线段
为线段![]() 的中点,点
的中点,点![]() 为线段
为线段![]() 的中点,连接
的中点,连接![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,延长![]() 至
至![]() ,使
,使![]() ,连接
,连接![]() 、
、![]() ,若
,若![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]()
【解析】
(1)利用待定系数法即可解决问题;
(2)根据三角形的中位线定理即可证明;
(3)如图2中,延长GF交AQ于K,连接PE.想办法证明AE=EH=BH,可得H(1,0),再证明PA=PH,可得PE⊥AH,设AE=EH=x,构建方程求出x即可解决问题.
(1)∵一次函数![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,
∴![]() ,
,![]() .
.
∵一次函数![]() 经过点
经过点![]() ,
,
∴![]() ,
,
∴一次函数的解析式为![]() .
.
(2)证明:如图1中,连接![]() .
.
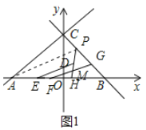
在![]() 中,∵
中,∵![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 中,∵
中,∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
(3)如图2中,延长![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
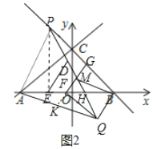
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,
∴![]() ,
,![]() ,可得
,可得![]() ,
,
∴![]() ,
,
∴![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() ,
,
设![]() ,
,
则![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】.Rt△ABC中,已知∠C=90°,∠B=50°,点D在边BC上,BD=2CD(图4).把△ABC绕着点D逆时针旋转m(0<m<180)度后,如果点B恰好落在初始Rt△ABC的边上,那么m=_________![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个三角形一条边的平方等于另两条的乘积,我们把这个三角形叫做比例三角形.
(1)已知![]() 是比例三角形,
是比例三角形,![]() ,
,![]() ,请直接写出所有满足条件的
,请直接写出所有满足条件的![]() 的长;
的长;
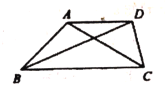
(2)如图,在四边形![]() 中,
中,![]() ,对角线
,对角线![]() 平分
平分![]() ,
,![]() .求证:
.求证:![]() 是比例三角形;
是比例三角形;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AC是矩形ABCD的对角线,AC的垂直平分线EF分别交BC、AD于点E和F,EF交AC于点O.
(1)求证:四边形AECF是菱形;(2)若AB=6,AD=8,求四边形AECF的周长.
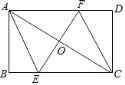
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 和
和![]() 是有公共顶点的直角三角形,
是有公共顶点的直角三角形,![]() ,点P为射线BD,CE的交点.
,点P为射线BD,CE的交点.
(1)如图1,若![]() 和
和![]() 是等腰三角形,求证:
是等腰三角形,求证:![]() ;
;
(2)如图2,若![]() ,问:(1)中的结论是否成立?请说明理由.
,问:(1)中的结论是否成立?请说明理由.
(3)在(1)的条件下,若![]() ,
,![]() ,若把
,若把![]() 绕点A旋转,当
绕点A旋转,当![]() 时,求PB的长.
时,求PB的长.
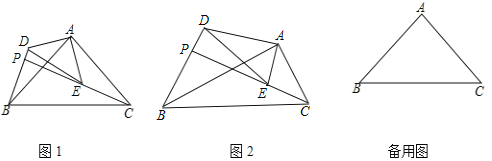
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中每个小正方形的边长均为1.线段AB的两个端点在小正方形的顶点上。
(1)在图中画一个以AB为腰的等腰三角形△ABC点C在小正方形的顶点上,且tan∠B=3;
(2)在图中画一个以AB为底的等腰三角形△ABD点D在小正方形的项点上,且△ABD是锐角三角形。连接CD,请直接写出线段CD的长。
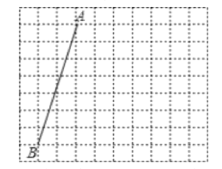
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小贤放学回家看到桌上有4块糖果,其中有玉米味、奶油味的糖果各1块,椰子味的糖果2块,这些糖果除味道外无其他差别.
(1)小贤随机地从盘中取出一块糖果,取出的是玉米味糖果的概率是多少?
(2)小贤随机地从盘中取出两块糖果,试用画树状图或列表的方法表示所有可能的结果,并求出小贤取出的两个都是椰子味糖果的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com