
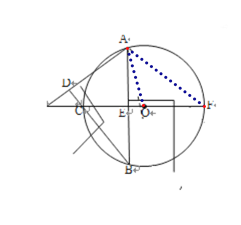
【题目】(本题8分)如图,⊙O是△ABC的外接圆,AD⊥BC于点D,直径CF⊥AB于点E,AD、FC的延长线交于点M。
(1)求证:EF=EM;
(2)若![]() ,AC=8,求sinM的值.
,AC=8,求sinM的值.

【答案】(1)答案见解析 (2)![]()
(1)证明:连AF,∵∠DCE=∠B+∠CEB=∠M+CDM而AD⊥BC于点D,CF⊥AB于点E,∴∠CEB=∠CDM∴∠B=∠M,又∵∠B=∠F,∴∠M=∠F,∴AM=AF又∵EF=EM
(2)解:连AO,∵CF为直径,AB⊥CF于点E,∴AE=BE∴CA=CB,∠B=∠BAC,而∠AOE=2∠B,∠ACD=∠B+∠BAC=2∠B∴∠ACD=∠AOE,又∵AD⊥BD,AE⊥CF,∴∠ADC=∠AEO
△ADC∽△AEO,∴![]() ,而AC=8,∴CF=2AO=12
,而AC=8,∴CF=2AO=12
∵CF为直径,∴∠CAF=90°,∴在Rt△CAF中
AF=![]() =
=![]() =4
=4![]() ,∴AM=4
,∴AM=4![]() ,易求
,易求
△OCA中AC上的高为2![]() ,用面积法求得AE=
,用面积法求得AE=![]() ,sinM=
,sinM=![]()
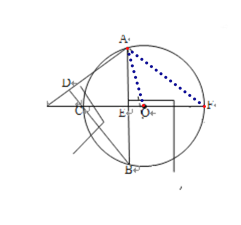
【解析】试题分析:本题考查了外角的性质,圆周角定理的推论,等腰三角形的判定与性质,垂径定理及其推论,相似三角形的判定与性质,勾股定理.
由三角形内角和得到∠B=∠M,由圆周角定理的推论可得∠B=∠F,从而∠M=∠F, △AMF是等腰三角形,由三线合一的性质可得EF=EM;
由垂径定理可得CA=CB,∠B=∠BAC,由圆周角定理的推论和外角性质可得∠ACD=∠AOE,进而证明△ADC∽△AEO,得到![]() ,求出CF的长,然后根据勾股定理求AF,面积法求AE,从而求sinM的值.
,求出CF的长,然后根据勾股定理求AF,面积法求AE,从而求sinM的值.
试题解析:
(1)证明:连AF,∵∠DCE=∠B+∠CEB=∠M+CDM而AD⊥BC于点D,CF⊥AB于点E,∴∠CEB=∠CDM∴∠B=∠M,又∵∠B=∠F,∴∠M=∠F,∴AM=AF又∵EF=EM
(2)解:连AO,∵CF为直径,AB⊥CF于点E,∴AE=BE∴CA=CB,∠B=∠BAC,而∠AOE=2∠B,∠ACD=∠B+∠BAC=2∠B∴∠ACD=∠AOE,又∵AD⊥BD,AE⊥CF,∴∠ADC=∠AEO
△ADC∽△AEO,∴![]() ,而AC=8,∴CF=2AO=12
,而AC=8,∴CF=2AO=12
∵CF为直径,∴∠CAF=90°,∴在Rt△CAF中
AF=![]() =
=![]() =4
=4![]() ,∴AM=4
,∴AM=4![]() ,易求
,易求
△OCA中AC上的高为2![]() ,用面积法求得AE=
,用面积法求得AE=![]() ,sinM=
,sinM=![]()


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,公路PQ和公路MN交于点P,且∠NPQ=45°,公路PQ上有一所学校A,AP=80![]() 米,现有一拖拉机在公路MN上以10米∕秒的速度行驶,拖拉机行驶时周围100米以内会受到噪声的影响,请判断拖拉机在行驶过程中是否对学校会造成影响,并说明理由,如果造成影响,求出造成影响的时间.
米,现有一拖拉机在公路MN上以10米∕秒的速度行驶,拖拉机行驶时周围100米以内会受到噪声的影响,请判断拖拉机在行驶过程中是否对学校会造成影响,并说明理由,如果造成影响,求出造成影响的时间.
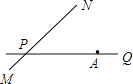
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁四人参加训练,近期的10次百米测试平均成绩都是13.2秒,方差如表
选手 | 甲 | 乙 | 丙 | 丁 |
方差(秒2) | 0.020 | 0.019 | 0.021 | 0.022 |
则这四人中发挥最稳定的是( )
A.甲
B.乙
C.丙
D.丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对本校学生为抗震救灾自愿捐款活动进行了抽样调查,得到了一组学生捐款情况的数据.下图是根据这组数据绘制的统计图,根据图表回答下列各问:
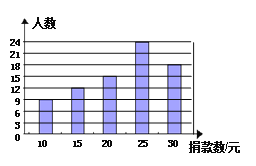
(1)求学校一共抽样调查的人数;
(2)求这组数据的众数、中位数;
(3)若该校共有1170名学生,估计全校学生共捐款多少元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AC、BD交于点M,过B、D两点分别作AC的垂线段BF、DE,AB=CD.
(1)若∠A=∠C,求证FM=EM;
(2)若FM=EM,则∠A=∠C.是真命题吗?(直接判断,不必证明)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校260名学生参加植树活动,要求每人植4﹣7棵,活动结束后随机抽查了20名学生每人的植树量,并分为四种类型,A:4棵;B:5棵;C:6棵;D:7棵,将各类的人数绘制成扇形图(如图1)和条形图(如图2).
回答下列问题:
(1)补全条形图;
(2)写出这20名学生每人植树量的众数、中位数;
(3)请你计算平均数,并估计这260名学生共植树多少棵?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com