
【题目】已知正方形ABCD和等腰Rt△BEF,BE=EF,∠BEF=90°,按图放置,使点E在BC上,取DF的中点G,连结EG、CG.
(1)请添加一条辅助线,构造一个和△FEG全等的三角形,并证明它们全等.
(2)探索EG、CG的数量关系和位置关系,并证明.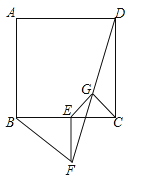
【答案】解:(1)延长EG交CD于点H,如图,则△DHG≌△FEG.证明如下:
∵∠BEF=90°,
∴EF⊥BC,
而CD⊥BC,
∴EF∥CD,
∴∠1=∠2,
∵点G为DF的中点,
∴DG=FG,
在△DHG和△FEG中,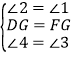 ,
,
∴△DHG≌△FEG(ASA);
(2)EG=CG,EG⊥CG.证明如下:
∵△DHG≌△FEG,
∴EF=DH,EG=HG,
∵BE=EF,
∴BE=DH,
∵CB=CD,
∴CD﹣DH=CB﹣BE,即CH=CE,
∴△CHE为等腰直角三角形,
∵EG=GH,
∴CG⊥EH,CG=EG=GH,
即EG=CG,EG⊥CG.
【解析】(1)延长EG交CD于点H,如图,先证明EF∥CD,则∠1=∠2,再由点G为DF的中点得到DG=FG,然后利用“ASA”判断△DHG≌△FEG;
(2)由△DHG≌△FEG得到EF=DH,EG=HG,而BE=EF,所以BE=DH,根据正方形的性质得CB=CD,则CH=CE,于是可判断△CHE为等腰直角三角形,然后根据等腰直角三角形的性质得到CG⊥EH,CG=EG=GH,即EG=CG,EG⊥CG.
【考点精析】解答此题的关键在于理解正方形的性质的相关知识,掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:
【题目】已知线段AB=20cm,M是线段AB的中点,C是线段AB延长线上的点,AC:BC=3:1,点D是线段BA延长线上的点,AD=AB.求:
(1)线段BC的长;
(2)线段DC的长;
(3)线段MD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简求值:(1)(3a2-8a)+(2a2-13a2+2a)-2(a3-3),其中a=-2;
(2)3x2y-![]() +3xy2,其中x=3,y=-
+3xy2,其中x=3,y=-![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
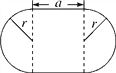
【题目】一个花坛的形状如图所示,它的两端是半径相等的半圆,求:
(1)花坛的周长l;
(2)花坛的面积S;
(3)若a=8m,r=5m,求此时花坛的周长及面积(π取3.14).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E在对角线AC上,点F在边BC上,联结BE、DF,DF交对角线于点P,且DE=DP.
(1)求证:AE=CP;
(2)求证:BE∥DF.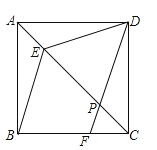
查看答案和解析>>
科目:初中数学 来源: 题型:
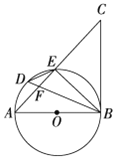
【题目】如图,AB是⊙O的直径,点D是弧AE上一点,且∠BDE=∠CBE,BD与AE交于点F.
(1)求证:BC是⊙O的切线;
(2)若BD平分∠ABE,求证:DE2=DF·DB;
(3)在(2)的条件下,延长ED,BA交于点P,若PA=AO,DE=2,求PD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com