
【题目】已知关于x的方程![]() .
.
(1)求证:无论k取何值,该方程总有实数根;
(2)若等腰![]() 的一边长
的一边长![]() ,另两边b、c恰好是该方程的两个根,求
,另两边b、c恰好是该方程的两个根,求![]() 的周长.
的周长.
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点![]() 经过某种变换后得到点
经过某种变换后得到点![]() ,我们把点
,我们把点![]() 叫做点
叫做点![]() 的终结点.已知点
的终结点.已知点![]() 的终结点为
的终结点为![]() ,点
,点![]() 的终结点为
的终结点为![]() ,点
,点![]() 的终结点为
的终结点为![]() ,这样依次得到
,这样依次得到![]() 、
、![]() 、
、![]() 、
、![]() 、…
、…![]() 、…,若点
、…,若点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为__________.
的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出下列命题:
①在直角三角形ABC中,已知两边长为3和4,则第三边长为5;
②三角形的三边a、b、c满足a2+c2=b2,则∠C=90°;
③△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC是直角三角形;
④△ABC中,若 a:b:c=1:2:![]() ,则这个三角形是直角三角形.
,则这个三角形是直角三角形.
其中,正确命题的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
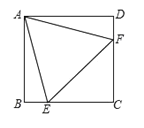
【题目】如图,在正方形ABCD中,边长为2的等边三角形AEF的顶点![]() 分别在BC和CD上,下列结论:
分别在BC和CD上,下列结论:
(1)BE=DF;(2)∠AEB=75°;(3)BE+DF=EF;(4)![]() .
.
其中正确的序号是____________(把你认为正确的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 满足条件:(1)在
满足条件:(1)在![]() 时,
时, ![]() 随
随![]() 的增大而增大,在
的增大而增大,在![]() 时,
时, ![]() 随
随![]() 的增大而减小;(2)与
的增大而减小;(2)与![]() 轴有两个交点,且两个交点间的距离小于
轴有两个交点,且两个交点间的距离小于![]() .以下四个结论:①
.以下四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,说法正确的个数有( )个
,说法正确的个数有( )个
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表数据是科研小组在某地区根据调查获取的:“距离地面的高度(千米)与此处的温度(摄氏度)”的关系。
距离地面高度/千米 | 0 | 1 | 2 | 3 | 4 | 5 |
温度/摄氏度 | 20 | 14 | 8 | 2 | -4 | -10 |
根据上表,请你回答:
(1)上表中___________是自变量;_________________是因变量;
(2)如果用![]() 表示距离地面的高度(千米),
表示距离地面的高度(千米),![]() 表示温度(摄氏度),请你写出
表示温度(摄氏度),请你写出![]() 与
与![]() 的关系式____________________________________;
的关系式____________________________________;
(3)请你利用(2)的结论,求该地区:①距离地面6.2千米的高空温度是多少?②当高空某处温度为-52度时,该处的高度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
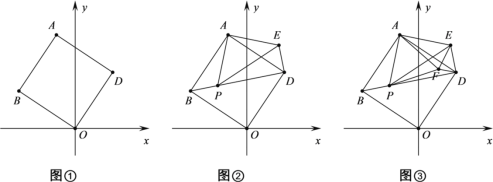
【题目】如图①,将正方形ABOD放在平面直角坐标系中,O是坐标原点,点D的坐标为(2,3),
(1)点B的坐标为 ;
(2)若点P为对角线BD上的动点,作等腰直角三角形APE,使∠PAE=90°,如图②,连接DE,则BP与DE的关系(位置与数量关系)是 ,并说明理由;
(3)在(2)的条件下,再作等边三角形APF,连接EF、FD,如图③,在 P点运动过程中当EF取最小值时,此时∠DFE= °;
(4)在(1)的条件下,点 M在 x 轴上,在平面内是否存在点N,使以 B、D、M、N为顶点的四边形是菱形?若存在,请求出点N的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线交AB于点E,交AC的延长线于点F.
(1)求证:DE⊥AB;
(2)若tan∠BDE=![]() , CF=3,求DF的长.
, CF=3,求DF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com