练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    (云南)从－1到1有3个整数，它们是：－1，0，1；从－2到2有5个整数，它们是：－2，－1，0，1，2；从－3到3有7个整数，它们是；－3，－2，－1，0，1，2，3；从－n到n(n为整数)，有________个整数．

    答案：2n+1
    提示：

    由已知条件探索规律


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    探究问题：
    （1）阅读理解：
    ①如图（A），在已知△ABC所在平面上存在一点P，使它到三角形顶点的距离之和最小，则称点P为△ABC的费马点，此时PA+PB+PC的值为△ABC的费马距离；
    ②如图（B），若四边形ABCD的四个顶点在同一圆上，则有AB•CD+BC•DA=AC•BD．此为托勒密定理；
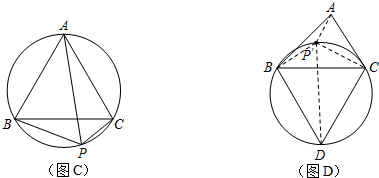
    精英家教网
    （2）知识迁移：
    ①请你利用托勒密定理，解决如下问题：
    如图（C），已知点P为等边△ABC外接圆的
    BC
    上任意一点．求证：PB+PC=PA；
    ②根据（2）①的结论，我们有如下探寻△ABC（其中∠A、∠B、∠C均小于120°）的费马点和费马距离的方法：
    第一步：如图（D），在△ABC的外部以BC为边长作等边△BCD及其外接圆；
    第二步：在
    BC
    上任取一点P′，连接P′A、P′B、P′C、P′D．易知P′A+P′B+P′C=P′A+（P′B+P′C）=P′A+
     
    ；
    第三步：请你根据（1）①中定义，在图（D）中找出△ABC的费马点P，并请指出线段
     
    的长度即为△ABC的费马距离．
    精英家教网
    （3）知识应用：
    2010年4月，我国西南地区出现了罕见的持续干旱现象，许多村庄出现了人、畜饮水困难，为解决老百姓的饮水问题，解放军某部来到云南某地打井取水．
    已知三村庄A、B、C构成了如图（E）所示的△ABC（其中∠A、∠B、∠C均小于120°），现选取一点P打水井，使从水井P到三村庄A、B、C所铺设的输水管总长度最小，求输水管总长度的最小值．
    精英家教网

    查看答案和解析>>

    科目：初中数学 来源： 题型：阅读理解

    从四川汶川地震到云南盈江地震，从海地地震到日本特大地震。近年来，地震在世界各地频频发生，给人类的生产和生活带来了重大影响。关于地震发生人类能否准确预测这个问题日益引起人们关注。据此回答18—21题。
    【小题1】3月11日日本地震发生之后，网上一则消息开始疯传，称此次地震，日本提前10秒就预测出来了。果真如此吗？3月12日，全国政协委员、中国地震局局长陈建民表示：“这是一个非常不专业的问题，所谓提前10秒预测出来，那是不可能的，也绝无此事……”陈局长对于预测地震可能性的明确表态是
    ①错误的，他否认了思维能正确认识存在 
    ②正确的，他做到了从当前科技水平的实际出发，实事求是 
    ③错误的，他否认了人能够发挥主观能动性去认识和发现客观规律 
    ④错误的，他否认了实践具有社会历史性
    A．①③④B．③④C．②④D．①③
    【小题2】地震发生时，会同时产生纵波和横波，纵波破坏力较小，但速度相对较快，横波破坏力较大但速度相对较慢。根据这一特性，地震预警系统可以提前数十秒对较远地区发出预警，为人们争取应对时间。材料蕴含的哲学道理是
    A．地震的成功预警来源于地震活动的规律性
    B．地震预警是人们改造客观规律的结果
    C．地震预警是一种客观的物质性活动，不受主观因素的制约
    D．认识地震规律的程度，决定着地震预警收到积极效果的程度
    【小题3】尽管地震预测难度很大，但全国政协委员、中科院院士、地球物理学家陈运泰认为，国际上对于地震预测确实存在不同看法，但普遍承认，地震长期预测还是有可行的办法，中期预测也有成功的例子，争论的焦点是短（期）临（震）预测。他建议，“十二五”规划草案中应该强化地震预测工作。关于地震的预测，下列说法错误的是
    A．认识具有无限性、上升性，终有一天人类能够做到预测地震
    B．规律是事物运动过程中固有的本质的必然的可变的联系，人能正确认识规律
    C．人的认识也是在不断发展的，因此人们能够在未来做到预测地震
    D．思维与存在具有同一性，因此人类会做到科学预测地震
    【小题4】2011年3月福岛核电站因地震发生核泄漏事故后，中国、法国、拉美等拥有核电站的国家纷纷检查本国的核设施安全，完善应对核事故的紧急预案。对核设施的安全检查活动进一步佐证 
    ①人类的好奇、兴趣和遐想是推进有关核安全认识的直接动力
    ②认识具有无限性，人们追求真理的过程是永无止境的过程
    ③认识具有创新性，核安全认识的进步以推翻已有理论为前提
    ④实践发展提出的客观需要是推进有关核安全认识的根本动力
    A．①②B．②③C．②④D．③④

    查看答案和解析>>

    科目：初中数学 来源：第1章《解直角三角形》中考题集（27）：1.3 解直角三角形（解析版） 题型：解答题

    探究问题：
    （1）阅读理解：
    ①如图（A），在已知△ABC所在平面上存在一点P，使它到三角形顶点的距离之和最小，则称点P为△ABC的费马点，此时PA+PB+PC的值为△ABC的费马距离；
    ②如图（B），若四边形ABCD的四个顶点在同一圆上，则有AB•CD+BC•DA=AC•BD．此为托勒密定理；

    （2）知识迁移：
    ①请你利用托勒密定理，解决如下问题：
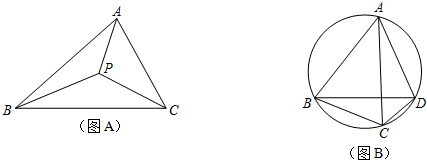
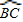    如图（C），已知点P为等边△ABC外接圆的上任意一点．求证：PB+PC=PA；
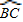    ②根据（2）①的结论，我们有如下探寻△ABC（其中∠A、∠B、∠C均小于120°）的费马点和费马距离的方法：
    第一步：如图（D），在△ABC的外部以BC为边长作等边△BCD及其外接圆；
    第二步：在上任取一点P′，连接P′A、P′B、P′C、P′D．易知P′A+P′B+P′C=P′A+（P′B+P′C）=P′A+______；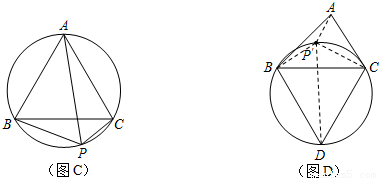
    第三步：请你根据（1）①中定义，在图（D）中找出△ABC的费马点P，并请指出线段______的长度即为△ABC的费马距离．

    （3）知识应用：
    2010年4月，我国西南地区出现了罕见的持续干旱现象，许多村庄出现了人、畜饮水困难，为解决老百姓的饮水问题，解放军某部来到云南某地打井取水．
    已知三村庄A、B、C构成了如图（E）所示的△ABC（其中∠A、∠B、∠C均小于120°），现选取一点P打水井，使从水井P到三村庄A、B、C所铺设的输水管总长度最小，求输水管总长度的最小值．

    查看答案和解析>>

    科目：初中数学 来源：2010年全国中考数学试题汇编《图形的旋转》（04）（解析版） 题型：解答题

    （2010•永州）探究问题：
    （1）阅读理解：
    ①如图（A），在已知△ABC所在平面上存在一点P，使它到三角形顶点的距离之和最小，则称点P为△ABC的费马点，此时PA+PB+PC的值为△ABC的费马距离；
    ②如图（B），若四边形ABCD的四个顶点在同一圆上，则有AB•CD+BC•DA=AC•BD．此为托勒密定理；

    （2）知识迁移：
    ①请你利用托勒密定理，解决如下问题：
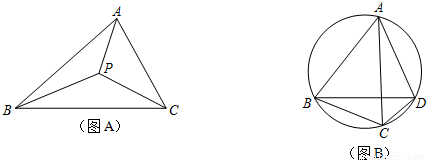
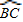    如图（C），已知点P为等边△ABC外接圆的上任意一点．求证：PB+PC=PA；
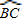    ②根据（2）①的结论，我们有如下探寻△ABC（其中∠A、∠B、∠C均小于120°）的费马点和费马距离的方法：
    第一步：如图（D），在△ABC的外部以BC为边长作等边△BCD及其外接圆；
    第二步：在上任取一点P′，连接P′A、P′B、P′C、P′D．易知P′A+P′B+P′C=P′A+（P′B+P′C）=P′A+______；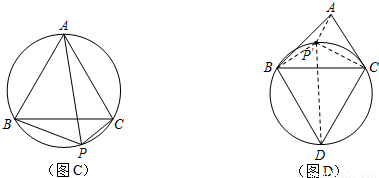
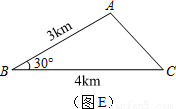
    第三步：请你根据（1）①中定义，在图（D）中找出△ABC的费马点P，并请指出线段______的长度即为△ABC的费马距离．

    （3）知识应用：
    2010年4月，我国西南地区出现了罕见的持续干旱现象，许多村庄出现了人、畜饮水困难，为解决老百姓的饮水问题，解放军某部来到云南某地打井取水．
    已知三村庄A、B、C构成了如图（E）所示的△ABC（其中∠A、∠B、∠C均小于120°），现选取一点P打水井，使从水井P到三村庄A、B、C所铺设的输水管总长度最小，求输水管总长度的最小值．

    查看答案和解析>>

    同步练习册答案