
【题目】已知二次函数y=﹣x2+(m﹣3)x+m.
(1)证明:不论m取何值,该函数图象与x轴总有两个公共点;
(2)若该函数的图象与y轴交于点(0,5),求出顶点坐标,并画出该函数图象.
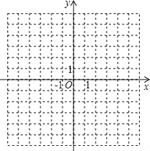
【答案】(1)见解析;(2)顶点坐标:(1,6);函数图像见解析.
【解析】
(1)证明对应的一元二次方程-x2+(m-3)x+m=0的根的判别式大于0,即可作出判断;
(2)把x=0,y=5代入抛物线的解析式,即可得到一个关于m的方程,从而求得m的值,得到函数的解析式,然后把解析式化成顶点式的形式,即可求解.
证明:(1)令y=0,﹣x2+(m﹣3)x+m=0
a=﹣1,b=m﹣3,c=m
b2﹣4ac=(m﹣3)2﹣4×(﹣1)m=m2﹣2m+9=(m﹣1)2+8
∵(m﹣1)2≥0
∴(m﹣1)2+8>0
∴b2﹣4ac>0
∴不论m取何值,该函数图象与x轴总有两个公共点.
(2)把x=0,y=5代入
∴m=5,
∴y=﹣x2+2x+5=﹣(x﹣1)2+6
顶点坐标:(1,6).


科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,OA=90cm,OB=30cm,一机器人在点B处看见一个小球从点A出发沿着AO方向匀速滚向点O,机器人立即从点B出发,沿直线匀速前进拦截小球,恰好在点C处截住了小球.如果小球滚动的速度与机器人行走的速度相等,那么机器人行走的路程BC是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
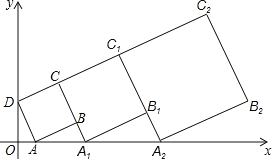
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2).延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1,按这样的规律进行下去,第2011个正方形(正方形ABCD看作第1个)的面积为( )
A.5(![]() )2010 B.5(
)2010 B.5(![]() )2010 C.5(
)2010 C.5(![]() )2011 D.5(
)2011 D.5(![]() )2011
)2011
查看答案和解析>>
科目:初中数学 来源: 题型:
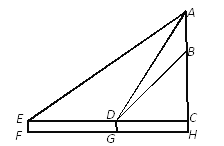
【题目】某学生为测量一棵大树AH及其树叶部分AB的高度,将测角仪放在F处测得大树顶端A的仰角为30°,放在G处测得大树顶端A的仰角为60°,树叶部分下端B的仰角为45°,已知点F、G与大树底部H共线,点F、G相距15米,测角仪高度为1.5米.求该树的高度AH和树叶部分的高度AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b的图象与反比例函数![]() 的图象相交于点A(2,3)和点B,与x轴相交于点C(8,0).
的图象相交于点A(2,3)和点B,与x轴相交于点C(8,0).
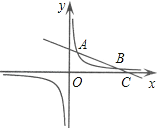
(1)求这两个函数的解析式;
(2)当x取何值时,y1>y2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个反比例函数y=![]() 和y=
和y=![]() 在第一象限内的图象如图所示,点P在y=
在第一象限内的图象如图所示,点P在y=![]() 的图象上,PC⊥x轴于点C,交y=
的图象上,PC⊥x轴于点C,交y=![]() 的图象于点A,PD⊥y轴于点D,交y=
的图象于点A,PD⊥y轴于点D,交y=![]() 的图象于点B,当点P在y=
的图象于点B,当点P在y=![]() 的图象上运动时,以下结论:①△ODB与△OCA的面积相等;②四边形PAOB的面积不会发生变化;③PA与PB始终相等;④当点A是PC的中点时,点B一定是PD的中点.其中一定正确的是( )
的图象上运动时,以下结论:①△ODB与△OCA的面积相等;②四边形PAOB的面积不会发生变化;③PA与PB始终相等;④当点A是PC的中点时,点B一定是PD的中点.其中一定正确的是( )
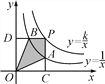
A. ①②③ B. ②③④ C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则结论:①PA平分∠RPS;②AS=AR;③QP∥AR;④△BRP≌△CSP.其中正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△OAB中,OA=OB,OA⊥OB.在△OCD中,OC=OD,OC⊥OD.
(1)如图1,若A,O,D三点在同一条直线上,求证:S△AOC=S△BOD;
(2)如图2,若A,O,D三点不在同一条直线上,△OAB和△OCD不重叠.则S△AOC=S△BOD是否仍成立?若成立,请予以证明;若不成立,也请说明理由.
(3)若A,O,D三点不在同一条直线上,△OAB和△OCD有部分重叠,经过画图猜想,请直接写出 S△AOC和S△BOD的大小关系.
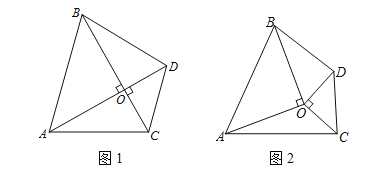
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图).已知该材料初始温度是32℃.
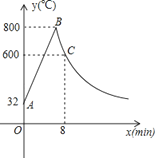
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作.那么锻造的操作时间有多长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com