
【题目】将一副三角板Rt△ABD与Rt△ACB(其中∠ABD=90°,∠D=60°,∠ACB=90°,∠ABC=45°)如图摆放,Rt△ABD中∠D所对直角边与Rt△ACB斜边恰好重合.以AB为直径的圆经过点C,且与AD交于点 E,分别连接EB,EC. 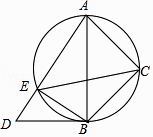
(1)求证:EC平分∠AEB;
(2)求 ![]() 的值.
的值.
【答案】
(1)证明:∵Rt△ACB中,∠ACB=90°,∠ABC=45°,
∴∠BAC=∠ABC=45°,
∵∠AEC=∠ABC,∠BEC=∠BAC,
∴∠AEC=∠BEC,
即EC平分∠AEB
(2)解:如图,设AB与CE交于点M.
∵EC平分∠AEB,
∴ ![]() =
= ![]() .
.
在Rt△ABD中,∠ABD=90°,∠D=60°,
∴∠BAD=30°,
∵以AB为直径的圆经过点E,
∴∠AEB=90°,
∴tan∠BAE= ![]() =
= ![]() ,
,
∴AE= ![]() BE,
BE,
∴ ![]() =
= ![]() =
= ![]() .
.
作AF⊥CE于F,BG⊥CE于G.
在△AFM与△BGM中,
∵∠AFM=∠BGM=90°,∠AMF=∠BMG,
∴△AFM∽△BGM,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() .
.
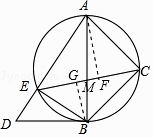
【解析】(1)由Rt△ACB中∠ABC=45°,得出∠BAC=∠ABC=45°,根据圆周角定理得出∠AEC=∠ABC,∠BEC=∠BAC,等量代换得出∠AEC=∠BEC,即EC平分∠AEB;(2)设AB与CE交于点M.根据角平分线的性质得出 ![]() =
= ![]() .易求∠BAD=30°,由直径所对的圆周角是直角得出∠AEB=90°,解直角△ABE得到AE=
.易求∠BAD=30°,由直径所对的圆周角是直角得出∠AEB=90°,解直角△ABE得到AE= ![]() BE,那么
BE,那么 ![]() =
= ![]() =
= ![]() .作AF⊥CE于F,BG⊥CE于G.证明△AFM∽△BGM,根据相似三角形对应边成比例得出
.作AF⊥CE于F,BG⊥CE于G.证明△AFM∽△BGM,根据相似三角形对应边成比例得出 ![]() =
= ![]() =
= ![]() ,进而求出
,进而求出 ![]() =
= ![]() =
= ![]() =
= ![]() .
.
【考点精析】本题主要考查了圆周角定理和相似三角形的判定与性质的相关知识点,需要掌握顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】为了了解某校九年级学生的跳高水平,随机抽取该年级50名学生进行跳高测试,并把测试成绩绘制成如图所示的频数表和未完成的频数直方图(每组含前一个边界值,不含后一个边界值).
某校九年级50名学生跳高测试成绩的频数表
组别(m) | 频数 |
1.09~1.19 | 8 |
1.19~1.29 | 12 |
1.29~1.39 | A |
1.39~1.49 | 10 |
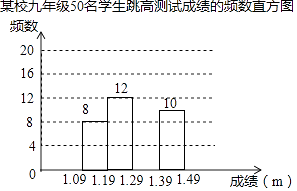
(1)求A的值,并把频数直方图补充完整;
(2)该年级共有500名学生,估计该年级学生跳高成绩在1.29m(含1.29m)以上的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+b(k≠0)的图象经过A(﹣1,﹣4),B(2,2)两点,P为反比例函数y= ![]() 图象上一动点,O为坐标原点,过点P作y轴的垂线,垂足为C,则△PCO的面积为( )
图象上一动点,O为坐标原点,过点P作y轴的垂线,垂足为C,则△PCO的面积为( )
A.2
B.4
C.8
D.不确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆直径,半径OC⊥AB于点O,D为半圆上一点,AC∥OD,AD与OC交于点E,连结CD、BD,给出以下三个结论:①OD平分∠COB;②BD=CD;③CD2=CECO,其中正确结论的序号是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题
(1)计算:6cos45°+( ![]() )﹣1+(
)﹣1+( ![]() ﹣1.73)0+|5﹣3
﹣1.73)0+|5﹣3 ![]() |+42017×(﹣0.25)2017
|+42017×(﹣0.25)2017
(2)先化简,再求值:( ![]() ﹣a+1)÷
﹣a+1)÷ ![]() +
+ ![]() ﹣a,并从﹣1,0,2中选一个合适的数作为a的值代入求值.
﹣a,并从﹣1,0,2中选一个合适的数作为a的值代入求值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某太阳能热水器的横截面示意图如图所示,已知真空热水管AB与支架CD所在直线相交于点O,且OB=OD,支架CD与水平线AE垂直,∠BAC=∠CDE=30°,DE=80cm,AC=165cm. 
(1)求支架CD的长;
(2)求真空热水管AB的长.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课桌生产厂家研究发现,倾斜12°﹣24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度的桌面.新桌面的设计图如图1所示,AB可绕点A旋转,在点C处安装一根可旋转的支撑臂CD,AC=30cm.
(1)如图2,当∠BAC=24°时,CD⊥AB,求支撑臂CD的长.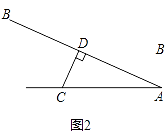
(2)如图3,当∠BAC=12°,求AD的长(结果保留根号).
[参考数据:sin24°=0.40,cos24°=0.91,tan24°=0.46,sin12°=0.20]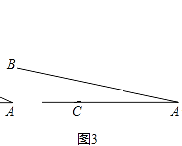
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y= ![]() x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为
x2经过平移得到抛物线y=ax2+bx,其对称轴与两段抛物线所围成的阴影部分的面积为 ![]() ,则a、b的值分别为( )
,则a、b的值分别为( ) 
A.![]() ,
, ![]()
B.![]() ,﹣
,﹣ ![]()
C.![]() ,﹣
,﹣ ![]()
D.﹣ ![]() ,
, ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com