
 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象信息解答:当出发几个小时后,两车相距为270km?
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象信息解答:当出发几个小时后,两车相距为270km? 分析 先利用路程除以时间求出慢车的速度,再利用相遇问题列式求解即可得到快车的速度,分相遇前相距270km和相遇后相距270km两种情况列出方程求解即可.
解答 解:由图象可得:慢车的速度为:450÷5=90km/h,
快车得速度为:$\frac{10}{3}×90÷(5-\frac{10}{3})$=180km/h,
所以,慢车速度为90km/h,
快车速度为180km/h;
由题意,可知两车行驶的过程中有2次两车之间的距离为270km.
即相遇前:(90+180)x=$\frac{10}{3}×(90+180)$-270,
解得x=$\frac{7}{3}$(h),
相遇后:(90+180)×(x-$\frac{7}{3}$)=270,
解得x=$\frac{10}{3}$(h),
故x=$\frac{7}{3}$ h或$\frac{10}{3}$ h,两车之间的距离为270km.
点评 本题考查了一次函数的应用,主要利用了路程、时间、速度三者之间的关系,要分相遇前与相遇后两种情况讨论,这也是本题容易出错的地方.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
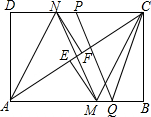 如图,在矩形ABCD中,把∠B、∠D分别翻折,使点B、D分别落在对角线BC上的点E、F处,折痕分别为CM、AN.连接MF、NE. P、Q是矩形的边CD、AB上的两点,连结PQ、CQ、MN.若PQ=CQ,PQ∥MN,且AB=4,BC=3,则PC的长度是2.
如图,在矩形ABCD中,把∠B、∠D分别翻折,使点B、D分别落在对角线BC上的点E、F处,折痕分别为CM、AN.连接MF、NE. P、Q是矩形的边CD、AB上的两点,连结PQ、CQ、MN.若PQ=CQ,PQ∥MN,且AB=4,BC=3,则PC的长度是2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
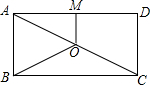 如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为( )
如图,O是矩形ABCD的对角线AC的中点,M是AD的中点,若AB=5,AD=12,则四边形ABOM的周长为( )| A. | 17 | B. | 18 | C. | 19 | D. | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com