
【题目】如图1,正方形ABCD中,点E是BC的中点,过点B作BG⊥AE于点G,过点C作CF垂直BG的延长线于点H,交AD于点F
(1)求证:△ABG≌△BCH;
(2)如图2,连接AH,连接EH并延长交CD于点I;
求证:① AB2=AE·BH;② 求![]() 的值;
的值;
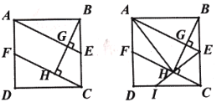
【答案】(1)见解析;(2)①见解析;②![]()
【解析】
(1)根据正方形的性质证得AB=BC,∠ABC=90°,根据垂直得到∠AGB=∠BHC=90°,再证明∠GAB=∠CBH即可得到结论;
(2)①根据两组角分别相等证明△ABE∽△BHC即可得到结论;
②证明四边形AECF是平行四边形得到AF=CE=![]() ,证明AH=AB,得到AH=2AF,证明△AFH∽△IHC得到
,证明AH=AB,得到AH=2AF,证明△AFH∽△IHC得到![]() ,连接AI,证明△AHI≌△ADI,得到
,连接AI,证明△AHI≌△ADI,得到![]() =
=![]() .
.
(1)∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠ABG+∠CBH=90°,
∵BG⊥AE,BH⊥CF,
∴∠AGB=∠BHC=90°,
∴∠GAB+∠ABG=90°,
∴∠GAB=∠CBH,
∴△ABG≌△BCH;
(2)①∵∠EAB=∠CBH,∠ABE=∠BHC=90°,
∴△ABE∽△BHC,
∴![]() ,
,
∵AB=BC,
∴AB2=AE·BH;
②∵AE⊥BH,CF⊥BH,
∴AE∥CF,
∵AF∥CE,
∴四边形AECF是平行四边形,
∴AF=CE=![]() ,
,
∵EH=![]() =BE,AE⊥BH,
=BE,AE⊥BH,
∴BG=GH,
∴AE垂直平分BH,
∴AH=AB=BC=2AF,
∴∠AHB=∠ABH=∠BCH,
∴∠AHF=∠HCI,
∵∠BAE=∠CBH,∠BAH=2∠BAE,∠CEI=2∠CBH,
∴∠BAH=∠CEI,
∴∠AFH=∠CIH,
∴△AFH∽△IHC,
∴![]() ,
,
连接AI,
∵∠ABH=∠AHB,∠EBH=∠EHB,
∴∠AHE=∠ABE=90°,
∴∠AHI=90°=∠D,
∵AH=AB=AD,AI=AI,
∴△AHI≌△ADI,
∴DI=HI,
∴![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,随着生活水平的提高,人们对饮水品质的需求越来越高.孝感市槐荫公司根据市场需求代理![]() 、
、![]() 两种型号的净水器,每台
两种型号的净水器,每台![]() 型净水器比每台
型净水器比每台![]() 型净水器进价多200元,用5万元购进
型净水器进价多200元,用5万元购进![]() 型净水器与用4.5万元购进
型净水器与用4.5万元购进![]() 型净水器的数量相等.
型净水器的数量相等.
(1)求每台![]() 型、
型、![]() 型净水器的进价各是多少元;
型净水器的进价各是多少元;
(2)槐荫公司计划购进![]() 、
、![]() 两种型号的净水器共50台进行试销,其中
两种型号的净水器共50台进行试销,其中![]() 型净水器为
型净水器为![]() 台,购买资金不超过9.8万元.试销时
台,购买资金不超过9.8万元.试销时![]() 型净水器每台售价2500元,
型净水器每台售价2500元,![]() 型净水器每台售价2180元.槐荫公司决定从销售
型净水器每台售价2180元.槐荫公司决定从销售![]() 型净水器的利润中按每台捐献
型净水器的利润中按每台捐献![]() 元作为公司帮扶贫困村饮水改造资金,设槐荫公司售完50台净水器并捐献扶贫资金后获得的利润为
元作为公司帮扶贫困村饮水改造资金,设槐荫公司售完50台净水器并捐献扶贫资金后获得的利润为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
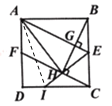
【题目】如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,点D是AB的中点,点P是直线BC上一点,将△BDP沿DP所在的直线翻折后,点B落在B1处,若B1D⊥BC,则点P与点B之间的距离为( )
A.1B.![]() C.1或 3D.
C.1或 3D.![]() 或5
或5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中国诗词大会”带着我们“赏中华诗词、寻文化基因、品生活之美”,从古人的智慧和情怀中汲取营养、涵养心灵,其中的“飞花令”环节,在广大青少年中圈粉无数.西安铁一中分校初三二班的同学们准备在班内举行“飞花令”比赛,组织过程如下:全班同学分成五个小组,每个小组派5名同学参加比赛,这5名同学依次从写有“春”、“云”、“月”、“花”、“夜”的五张卡片中随机摸出一张(不放回),5个小组中抽取相同字的同学进行比赛(例如5名抽到“春”字同学进行以“春”为主题字的飞花令比赛).第一小组的小丽和第二小组的小英分别是各自小组第一个抽取卡片的同学.
(1)求小丽抽到“春”的概率;
(2)小丽和小英都比较擅长“春”和“月”为主题的诗句,求她们至少有一人抽到自己擅长的主题字的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2+2ax-3与x轴交于A、B(1,0)两点(点A在点B的左侧),与y轴交于点C,将抛物线沿y轴平移m(m>0)个单位,当平移后的抛物线与线段OA有且只有一个交点时,则m的取值范围是_______________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形都是由面积为1的正方形按一定的规律组成的,其中,第1个图形中面积为1的正方形有9个,第2个图形中面积为1的正方形有14个,……,按此规律,则第几个图形中面积为1的正方形的个数为2019个( )
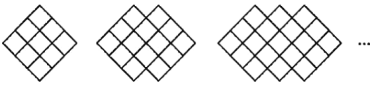
A.400B.401C.402D.403
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 的中点.
的中点.
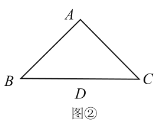
(1)如图①,若点![]() 分别为
分别为![]() 上的点,且
上的点,且![]() ,试探究
,试探究![]() 和
和![]() 的数量关系;并说明四边形
的数量关系;并说明四边形![]() 的面积是定值吗?若是,请求出;若不是,请说明理由.
的面积是定值吗?若是,请求出;若不是,请说明理由.
(2)若点![]() 分别为
分别为![]() 延长线上的点,且
延长线上的点,且![]() ,那么
,那么![]() 吗?请利用图②说明理由.
吗?请利用图②说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 是
是![]() 上一点,且
上一点,且![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
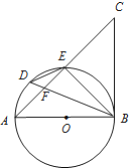
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,求证:
,求证:![]() 是
是![]() 的平分线;
的平分线;
(3)在(2)的条件下,延长![]() ,
,![]() 交与点
交与点![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
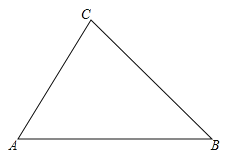
【题目】如图,已知△ABC,请用直尺(不带刻度),和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹).
(1)作菱形AMNP,使点M,N、P在边AB、BC、CA上;
(2)当∠A=60°,AB=8,AC=6时,求菱形AMNP的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com