
 已知如图,在平面直角坐标系中,四边形ABCD的顶点A,B在第一象限,AB∥x轴,∠B=90°,AB+OC=OA,OD平分∠AOC交BC于点D.若四边形ABDO的面积为4,反比例函数y=$\frac{k}{x}$的图象经过点D,点A,则k的值是( )
已知如图,在平面直角坐标系中,四边形ABCD的顶点A,B在第一象限,AB∥x轴,∠B=90°,AB+OC=OA,OD平分∠AOC交BC于点D.若四边形ABDO的面积为4,反比例函数y=$\frac{k}{x}$的图象经过点D,点A,则k的值是( )| A. | 8 | B. | 6 | C. | 3 | D. | 4 |
分析 首先根据角平分线的性质得出DE=DC,进而利用HL定理得出Rt△ODE≌Rt△ODC以及Rt△ADE≌Rt△ADB,求出A,D点坐标关系,进而得出k的值.
解答  解:过点D作DE⊥AO于点E,连接AD,
解:过点D作DE⊥AO于点E,连接AD,
∵梯形ABCD的顶点A,B在第一象限,AB∥x轴,∠B=90°,
∴∠OCB=90°,
∵OD平分∠AOC交BC于点D,
∴DE=DC,
在Rt△ODE和Rt△ODC中,
$\left\{\begin{array}{l}{DO=DO}\\{DE=DC}\end{array}\right.$,
∴Rt△ODE≌Rt△ODC(HL),
∴EO=CO,
又∵AB+OC=OA,
∴AE=AB,
在Rt△ADE和Rt△ADB中
$\left\{\begin{array}{l}{AD=AD}\\{AE=AB}\end{array}\right.$,
∴Rt△ADE≌Rt△ADB(HL),
∴BD=ED,
∴BD=CD=ED,
∵反比例函数y=$\frac{k}{x}$的图象过点D,点A,
∴设D点坐标为(a,b),则B(a,2b),
∴A($\frac{a}{2}$,2b),
即AB=AE=$\frac{a}{2}$,CO=OE=a,
∵DE=b,则BD=b,
∴S四边形ABDO=S△ADO+S△ABD=$\frac{1}{2}$b(a+$\frac{1}{2}$a)+$\frac{1}{2}$b×$\frac{1}{2}$a=$\frac{1}{2}$b×2a=ab=4,
∵D(a,b),
∴ab=k=4.
故选D.
点评 主要考查了全等三角形的判定性质以及反比例函数图象上点的坐标性质和角平分线的性质等知识,根据题意得出A,D点坐标是解题关键.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:选择题
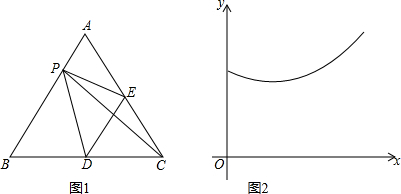
| A. | 线段PD | B. | 线段PC | C. | 线段PE | D. | 线段DE |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
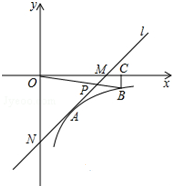 如图,在平面直角坐标系中,直线l与x轴相交于点M(3,0),与y轴相交于点N(0,-4),反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段MN的中点A,
如图,在平面直角坐标系中,直线l与x轴相交于点M(3,0),与y轴相交于点N(0,-4),反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段MN的中点A,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
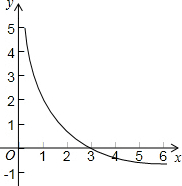 小颖画了一个函数y=$\frac{a}{x}$-1的图象如图,那么关于x的分式方程$\frac{a}{x}$=1的解是( )
小颖画了一个函数y=$\frac{a}{x}$-1的图象如图,那么关于x的分式方程$\frac{a}{x}$=1的解是( )| A. | x=1 | B. | x=2 | C. | x=3 | D. | x=4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 快、慢两车分别从相距120千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,快车到达乙地后,立即按原路返回,返回时的速度是去时速度的2倍,结果与慢车同时回到甲地.慢车距出发地的路程y1(千米)与出发后所用的时间x(小时)的关系如图所示.
快、慢两车分别从相距120千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,快车到达乙地后,立即按原路返回,返回时的速度是去时速度的2倍,结果与慢车同时回到甲地.慢车距出发地的路程y1(千米)与出发后所用的时间x(小时)的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com