
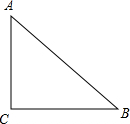
 ��ͼ����Rt��ABC�У���C=90�㣬AC=6��BC=8������һ��O�ӵ�A��������AB�����˶����������Bʱ���˶�ֹͣ���Ե�OΪԲ�ģ�rΪ�뾶��Բ��Ϊ��O��
��ͼ����Rt��ABC�У���C=90�㣬AC=6��BC=8������һ��O�ӵ�A��������AB�����˶����������Bʱ���˶�ֹͣ���Ե�OΪԲ�ģ�rΪ�뾶��Բ��Ϊ��O������ ��1��������ACB��ƽ���߽�ABһ�㣬�˵������ֱ��AC��BC����ʱ��Բ��O��
����֤���ı���OECF�������Σ�Ȼ�����ƽ���߷��߶γɱ�������������ã�
��2���ٸ��ݣ�1�����ɵõ����ۣ�
���ɣ�1����õĽ�����ͼ�μ��ɵõ����ۣ�
��� �⣺��1��������ACB��ƽ���߽�ABһ�㣬�˵������ֱ��AC��BC����ʱ��Բ��O��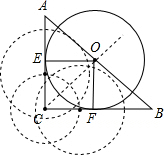
����AC�ϵ��е�ΪE��BC�ϵ��е�ΪF��
��OE=OF=r����C=��CEO=��CFO=90�㣬
���ı���OECF�������Σ�
��CE=CF=r��
��OE��BC��
��$\frac{OE}{BC}$=$\frac{AE}{AC}$��
��$\frac{r}{8}$=$\frac{6-r}{6}$��
���r=$\frac{24}{7}$��
��2�٣��ɣ�1���ڿ�֪��r=3ʱ����O�����ABC��AC�����У�
������O�Ⱥ�ֱ��BC���У��ٺ�ֱ��AC���У���r�ķ�Χ��$\frac{24}{7}$��r��6��
���� ���⿼�����ֱ����Բ��λ�ù�ϵ�Լ����ߵ����ʣ�����Բ�ĵ�ֱ�ߵľ������Բ�İ뾶ʱ��ֱ����Բ�����ǽ���Ĺؼ���


 ��ٽ������½������������ϵ�д�
��ٽ������½������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
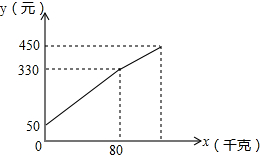 ���ү��ÿǧ��2.1Ԫ������һ�����ٵ����ϳ��ۣ�Ϊ�˷��㣬������һЩ��Ǯ���ã����Ȱ��г����۳�һЩ���ֽ��ͳ��ۣ��۳�����ǧ����x�������г��е�Ǯ��yԪ����������Ǯ���Ĺ�ϵ��ͼ��ʾ�����ͼ��ش��������⣺
���ү��ÿǧ��2.1Ԫ������һ�����ٵ����ϳ��ۣ�Ϊ�˷��㣬������һЩ��Ǯ���ã����Ȱ��г����۳�һЩ���ֽ��ͳ��ۣ��۳�����ǧ����x�������г��е�Ǯ��yԪ����������Ǯ���Ĺ�ϵ��ͼ��ʾ�����ͼ��ش��������⣺�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
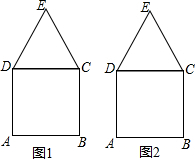 ��ͼ����֪������ABCD�͵ȱ�������CDE���밴Ҫ��������л�ͼ��Ҫ�ٽ����̶ȵ�ֱ�ߣ��ڱ�����Ҫ�Ļ�ͼ�ۼ���
��ͼ����֪������ABCD�͵ȱ�������CDE���밴Ҫ��������л�ͼ��Ҫ�ٽ����̶ȵ�ֱ�ߣ��ڱ�����Ҫ�Ļ�ͼ�ۼ����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
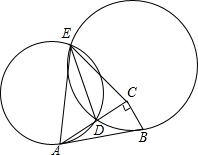 ����ֱ��������ABC����D��AC��������һ�㣮����Բ��ֱ��AB�ֱ������ڵ�A��B��������Բ����D��E���㣮��֤����BAC=��DEC��
����ֱ��������ABC����D��AC��������һ�㣮����Բ��ֱ��AB�ֱ������ڵ�A��B��������Բ����D��E���㣮��֤����BAC=��DEC���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2-x}{1-x}$ | B�� | x+1 | C�� | x-1 | D�� | $\frac{1}{2-x}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com