
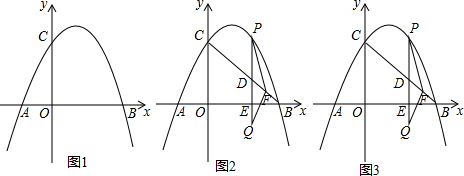
分析 (1)先确定A点坐标,然后把A点和B点坐标代入解析式得到关于a和h的方程组,然后解方程组;
(2)抛物线解析式为y=-$\frac{2}{9}$x2+$\frac{4}{3}$x+6,则C(0,6),再利用待定系数法求出直线BC的解析式为y=-$\frac{2}{3}$x+6,根据二次函数图象上点的坐标特征与一次函数图象上点的坐标特征,设P(t,-$\frac{2}{9}$t2+$\frac{4}{3}$t+6),D(t,-$\frac{2}{3}$t+6),所以PD=-$\frac{2}{9}$t2+2t;作PH⊥BC于H,如图2,在Rt△OBC中利用勾股定理计算出BC=3$\sqrt{13}$,接着证明Rt△FDQ∽Rt△OCB得到DF=$\frac{2\sqrt{13}}{13}$DQ,证明Rt△PDH∽Rt△BCO得到PH=$\frac{3\sqrt{13}}{13}$PD,DH=$\frac{2\sqrt{13}}{13}$PD,所以HF=$\frac{2\sqrt{13}}{13}$PQ=$\frac{16\sqrt{13}}{13}$,而PD=$\frac{\sqrt{13}}{5}$PF,于是在Rt△PHF中利用勾股定理得到($\frac{3\sqrt{13}}{13}$PD)2+($\frac{16\sqrt{13}}{13}$)2=($\frac{5\sqrt{13}}{13}$PD)2,解得PD=4,则-$\frac{2}{9}$t2+2t=4,解得t=3(舍去)或t=6,所以点P的坐标为(6,6);
(3)在(2)的条件下,确定点P、E、Q、D的坐标,根据P、C的坐标可知PCOE是正方形,由于∠GOQ=45°,于是联想到“90度含45度”模型,过O点作OF⊥OQ交CP于F,连接FG,易证△COF≌△EOQ和△FOG≌△QOG,利用勾股定理算出EG的长度,进而确定R点坐标,由RH=QR可知H与Q关于R点对称,于是得出H点坐标,从而算出AH的长度,将H点的坐标代入抛物线解析式验证即可判定H点是否在抛物线上.
解答 解:(1)∵AB=12,B(9,0),
∴A(-3,0),
把A(-3,0),B(9,0)代入y=a(x-h)2+8得$\left\{\begin{array}{l}{a(-3-h)^{2}+8=0}\\{a(9-h)^{2}+8=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{2}{9}}\\{h=3}\end{array}\right.$;
(2)抛物线解析式为y=a(x-h)2+8=-$\frac{2}{9}$(x-3)2+8=-$\frac{2}{9}$x2+$\frac{4}{3}$x+6,
当x=0时,y=-$\frac{2}{9}$x2+$\frac{4}{3}$x+6=6,则C(0,6),
设直线BC的解析式为y=mx+n,把C(0,6),B(9,0)代入得$\left\{\begin{array}{l}{n=6}\\{9m+n=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{m=-\frac{2}{3}}\\{n=6}\end{array}\right.$,
∴直线BC的解析式为y=-$\frac{2}{3}$x+6,
设P(t,-$\frac{2}{9}$t2+$\frac{4}{3}$t+6),则D(t,-$\frac{2}{3}$t+6),
∴PD=-$\frac{2}{9}$t2+$\frac{4}{3}$t+6-(-$\frac{2}{3}$t+6)=-$\frac{2}{9}$t2+2t,
作PH⊥BC于H,如图2,
在Rt△OBC中,OC=6,OB=9,BC=$\sqrt{{6}^{2}+{9}^{2}}$=3$\sqrt{13}$,
∵PE⊥x轴,
∴DQ∥OC,
∴∠QDF=∠OCB,
∴Rt△FDQ∽Rt△OCB,
∴$\frac{DF}{OC}$=$\frac{DQ}{BC}$,即$\frac{DF}{6}$=$\frac{DQ}{3\sqrt{13}}$,
∴DF=$\frac{2\sqrt{13}}{13}$DQ,
同理可得Rt△PDH∽Rt△BCO,
∴$\frac{PH}{OB}$=$\frac{DH}{OC}$=$\frac{PD}{BC}$,即$\frac{PH}{9}$=$\frac{DH}{6}$=$\frac{PD}{3\sqrt{13}}$,
∴PH=$\frac{3\sqrt{13}}{13}$PD,DH=$\frac{2\sqrt{13}}{13}$PD,
∴HF=HD+DF=$\frac{2\sqrt{13}}{13}$DQ+$\frac{2\sqrt{13}}{13}$PD=$\frac{2\sqrt{13}}{13}$(DQ+PD)=$\frac{2\sqrt{13}}{13}$PQ=$\frac{2\sqrt{13}}{13}$×8=$\frac{16\sqrt{13}}{13}$,
∵PD=$\frac{\sqrt{13}}{5}$PF,
∴PF=$\frac{5\sqrt{13}}{13}$PD,
在Rt△PHF中,∵PH2+HF2=PF2,
∴($\frac{3\sqrt{13}}{13}$PD)2+($\frac{16\sqrt{13}}{13}$)2=($\frac{5\sqrt{13}}{13}$PD)2,解得PD=4,
∴-$\frac{2}{9}$t2+2t=4,解得t=3(舍去)或t=6,
∴点P的坐标为(6,6);
(3)如图3,
由(2)可知:P(6,6)、D(6,2)、E(6,0)、Q(6,-2),
连接CP,过O点作OF⊥OQ交CP于F,连接FG,
∵C(0,6),
∴OQPC为正方形,
∴∠COF=∠EOQ,
在△COF和△EOQ中,
$\left\{\begin{array}{l}{∠FCO=∠QEO}\\{CO=EO}\\{∠COF=∠EOQ}\end{array}\right.$,
∴△COF≌△EOQ(ASA),
∴CF=EQ=2,OF=OQ,
∴PF=6-2=4,
在△FOG和△QOG中,
$\left\{\begin{array}{l}{FO=QO}\\{∠FOG=∠QOG}\\{OG=OG}\end{array}\right.$,
∴△FOG≌△QOG(SAS),
∴FG=QG,
∴FG=CF+GE,
设GE=x,则PG=6-x,FG=2+x,
在Rt△PFG中,由勾股定理可得:16+(6-x)2=(2+x)2,
解得x=3,
∴G为PE中点,GQ=5,
∵GR∥x轴,
∴R($\frac{9}{2}$,3)
∵RH=QR,
∴H(3,8),
∴AH=10,
经验证,H点的坐标满足抛物线的方程,
∴H点在抛物线上.
点评 本题为二次函数的综合题,主要考查了二次函数图象上点的坐标特征、一次函数图象上点的坐标特征和二次函数的性质、待定系数法求函数解析式、相似三角形的判定与性质、全等三角形的判定与性质、勾股定理等重要知识点,难度较大.判断出PCOE是正方形并利用90度含45度模型构造全等三角形是解决第(3)问的关键.


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
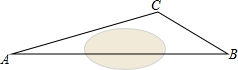 在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.如图,现测得∠ABC=30°,∠CAB=15°,AC=200米,请计算A,B两个凉亭之间的距离(结果精确到1米)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)
在一次课外实践活动中,同学们要测量某公园人工湖两侧A,B两个凉亭之间的距离.如图,现测得∠ABC=30°,∠CAB=15°,AC=200米,请计算A,B两个凉亭之间的距离(结果精确到1米)(参考数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
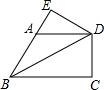 如图,在四边形ABCD中,∠ABC=60°,∠BAD=120°,∠ADC=90°,对角线BD平分∠ABC,过点D作DE⊥BA,交BA的延长线于点E.若AD=2,则四边形BCDE的周长为( )
如图,在四边形ABCD中,∠ABC=60°,∠BAD=120°,∠ADC=90°,对角线BD平分∠ABC,过点D作DE⊥BA,交BA的延长线于点E.若AD=2,则四边形BCDE的周长为( )| A. | 6+$\sqrt{3}$ | B. | 6+2$\sqrt{3}$ | C. | 7+$\sqrt{3}$ | D. | 7+2$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com