练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．计算-$\sqrt{（-3）^{2}}$的结果是-3．

    分析 根据二次根式的性质化简即可．

    解答 解：-$\sqrt{（-3）^{2}}$=-|-3|=-3
    故答案为：-3．

    点评 本题考查的是二次根式的化简，掌握二次根式的性质是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    1．如图，正方形OABC的顶点O在坐标原点，顶点A的坐标为（4，3）
    （1）顶点C的坐标为（-3，4），顶点B的坐标为（1，7）；
    （2）现有动点P、Q分别从C、A同时出发，点P沿线段CB向终点B运动，速度为每秒1个单位，点Q沿折线A→O→C向终点C运动，速度为每秒k个单位，当运动时间为2秒时，以P、Q、C为顶点的三角形是等腰三角形，求此时k的值．
    （3）若正方形OABC以每秒$\frac{5}{3}$个单位的速度沿射线AO下滑，直至顶点C落到x轴上时停止下滑．设正方形OABC在x轴下方部分的面积为S，求S关于滑行时间t的函数关系式，并写出相应自变量t的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

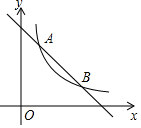    1．如图，一次函数y=-x+3的图象与反比例y=$\frac{k}{x}$（k为常数，且k≠0）的图象交于A（1，a），B两点．
    （1）求反比例函数的表达式及点B的坐标；
    （2）在x轴上找一点P，使PA+PB的值最小，求满足条件的点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．爸爸为了检查小明对平行线的条件与性质这部分知识的掌握情况，给他出了一道题：如图，AB∥DE，∠B=80°，CM平分∠BCD，CN⊥CM，求∠NCE的度数．小明稍加思索，就做出来了，你知道他是怎样解的吗？请把你的推理过程写下来吧．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．计算：
    （1）（-3）2-$\sqrt{4}$+（$\frac{1}{2}$）-1．
    （2）（x+1）2-2（x-2）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．如图，在四边形ABCD中，AD∥BC，∠B﹦90°，AB﹦8cm，AD﹦24cm，BC﹦26cm，点p从点A出发，以1cm/s的速度向点D运动；点Q从点C同时出发，以3cm/s的速度向点B运动，规定其中一个动点到达端点时，另一个动点也随之停止运动．设运动时间为t s．
    （1）t为何值时，四边形PQCD为平行四边形？
    （2）t为何值时，四边形PQCD为等腰梯形？（等腰梯形的两腰相等，两底角相等）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

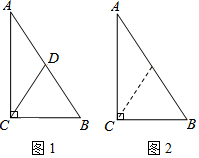    2．用两种方法证明“直角三角形斜边上的中线等于斜边的一半”．
    已知：如图1，在Rt△ABC中，∠ACB=90°，CD是斜边AB上的中线．
    求证：CD=$\frac{1}{2}$AB．
    证法1：如图2，在∠ACB的内部作∠BCE=∠B，
    CE与AB相交于点E．
    ∵∠BCE=∠B，
    ∴①．
    ∵∠BCE+∠ACE=90°，
    ∴∠B+∠ACE=90°．
    又∵②，
    ∴∠ACE=∠A．
    ∴EA=EC．
    ∴EA=EB=EC，
    即CE是斜边AB上的中线，且CE=$\frac{1}{2}$AB．
    又∵CD是斜边AB上的中线，即CD与CE重合，
    ∴CD=$\frac{1}{2}$AB．
    请把证法1补充完整，并用不同的方法完成证法2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．化简：
    （1）$\frac{1}{x-3}$-$\frac{6}{{x}^{2}-9}$
    （2）$\frac{{x}^{2}-x}{{x}^{2}+2x+1}$÷$\frac{x-1}{x+1}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

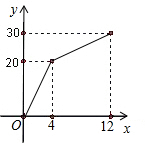    17．有一个附有进出水管的容器，每单位时间内进出的水量都是一定的，设从某时
    刻开始的4分钟内只进水，不出水，在随后的8分钟内既进水又出水，得到时间x（分）与水量y（升）之间的关系如图所示．
    （1）每分钟进水多少？
    （2）4≤x≤12时，x与y有何关系？
    （3）若12分钟后只放水，不进水，求y的表达式．

    查看答案和解析>>

    同步练习册答案