
分析 先表示A、B两点的坐标,列方程组可表示交点C、D的坐标,根据两点距离公式表示AC和BD的长,可得结论.
解答 解:由题意得:A(-$\frac{b}{k}$,0),B(0,b),
由$\left\{\begin{array}{l}{y=\frac{1}{x}}\\{y=kx+b}\end{array}\right.$得:kx2+bx-1=0,
x=$\frac{-b±\sqrt{{b}^{2}+4k}}{2k}$,
∴C($\frac{-b-\sqrt{{b}^{2}+4k}}{2k}$,$\frac{b-\sqrt{{b}^{2}+4k}}{2}$),D($\frac{-b+\sqrt{{b}^{2}+4k}}{2k}$,$\frac{b+\sqrt{{b}^{2}+4k}}{2}$),
∴AC=$\sqrt{(\frac{-b-\sqrt{{b}^{2}+4k}}{2k}+\frac{b}{k})^{2}+(\frac{b-\sqrt{{b}^{2}+4k}}{2})^{2}}$=$\sqrt{(\frac{b-\sqrt{{b}^{2}+4k}}{2k})^{2}+(\frac{b-\sqrt{{b}^{2}+4k}}{2})^{2}}$,
BD=$\sqrt{(\frac{-b+\sqrt{{b}^{2}+4k}}{2k})^{2}+(\frac{b+\sqrt{{b}^{2}+4k}}{2}-b)^{2}}$=$\sqrt{(\frac{b-\sqrt{{b}^{2}+4k}}{2k})^{2}+(\frac{b-\sqrt{{b}^{2}+4k}}{2})^{2}}$,
∴AC=BD.
点评 本题考查了函数与坐标轴的交点及两函数的交点问题、两点距离公式,熟练掌握两点距离公式是关键.


科目:初中数学 来源: 题型:选择题
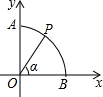 如图,以坐标原点O为圆心,半径为1的弧交坐标轴于A,B两点,P是$\widehat{AB}$上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )
如图,以坐标原点O为圆心,半径为1的弧交坐标轴于A,B两点,P是$\widehat{AB}$上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )| A. | (sinα,sinα) | B. | (cosα,cosα) | C. | (sinα,cosα) | D. | (cosα,sinα) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
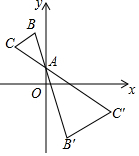 如图,在坐标系中,以A(0,2)为位似中心,在y轴右侧作△ABC放大2倍后的位似图形△AB'C',若C的对应点C'的坐标为(m,n),则点C的坐标为( )
如图,在坐标系中,以A(0,2)为位似中心,在y轴右侧作△ABC放大2倍后的位似图形△AB'C',若C的对应点C'的坐标为(m,n),则点C的坐标为( )| A. | ($-\frac{1}{2}$m,$-\frac{1}{2}$n+3) | B. | ($-\frac{1}{2}$m,$-\frac{1}{2}$n-3) | C. | ($-\frac{1}{2}$m,$-\frac{1}{2}$n+2) | D. | ($-\frac{1}{2}$m,$-\frac{1}{2}$n-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
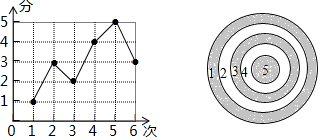 一种游戏如图,在一个定点位置用球拍扫动滑块,滑块落在圆环形靶图的相应位置,可以得到相应的分数.江小颖做6次的成绩如左图,对于这组数据,说法中不正确的是( )
一种游戏如图,在一个定点位置用球拍扫动滑块,滑块落在圆环形靶图的相应位置,可以得到相应的分数.江小颖做6次的成绩如左图,对于这组数据,说法中不正确的是( )| A. | 平均数3 | B. | 中位数3 | C. | 方差是2.5 | D. | 众数是3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com