
【题目】在纪念中国抗日战争胜利70周年之际,某公司决定组织员工观看抗日战争题材的影片,门票有甲乙两种,甲种票比乙种票每张贵6元;买甲种票10张,乙种票15张共用去660元.
(1)求甲、乙两种门票每张各多少元?
(2)如果公司准备购买35张门票且购票费用不超过1000元,那么最多可购买多少张甲种票?
【答案】
(1)解:设乙种门票每张x元,则甲种门票每张(x+6)元,根据题意得
10(x+6)+15x=660,
解得x=24.
答:甲、乙两种门票每张各30元、24元
(2)解:设可购买y张甲种票,则购买(35﹣y)张乙种票,根据题意得
30y+24(35﹣y)≤1000,
解得y≤26 ![]() .
.
答:最多可购买26张甲种票
【解析】(1)设乙种门票每张x元,则甲种门票每张(x+6)元,根据“买甲种票10张,乙种票15张共用去660元”列方程即可求解;(2)设可购买y张甲种票,则购买(35﹣y)张乙种票,根据购票费用不超过1000元列出不等式即可求解.本题考查了一元一次方程与一元一次不等式的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的关系,列出方程或不等式,再求解.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
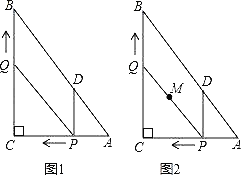
【题目】如图1,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C以1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度运动,过点P作PD∥BC,交AB于点D,连接PQ分别从点A、C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
(1)直接用含t的代数式分别表示:QB= ,PD= .
(2)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由.并探究如何改变Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度;
(3)如图2,在整个运动过程中,求出线段PQ中点M所经过的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知∠ABC=60°,EF⊥AB,垂足为F,连接DF. 
(1)求证:△ABC≌△EAF;
(2)试判断四边形EFDA的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是等边三角形ABC内的一点,且PA=3,PB=3,PC=5,以BC为边在△ABC外作△BQC≌△BPA,连接PQ,则以下结论错误的是()

A. △BPQ是等边三角形 B. △PCQ是直角三角形 C. ∠APB=150° D. ∠APC=135°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,有一个等腰直角三角形AOB,∠OAB=90°,直角边AO在x轴上,且AO=1.将Rt△AOB绕原点O顺时针旋转90°得到等腰直角三角形A1OB1,且A1O=2AO,再将Rt△A1OB1绕原点O顺时针旋转90°得到等腰三角形A2OB2,且A2O=2A1O…,依此规律,得到等腰直角三角形A2017OB2017.则点B2017的坐标_______

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠A=∠B,AE=BE,点D在AC边上,∠1=∠2,AE和BD相交于点O,若∠1=38°,则∠BDE的度数为( )

A. 71° B. 76° C. 78° D. 80°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com