
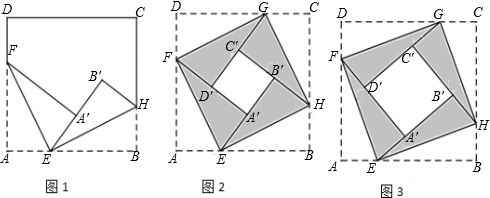
分析 (1)根据折叠的性质得到△A′EF≌△AEF,△B′EH≌△BEH,根据全等三角形的性质得到AE=A′E,BE=B′E,∠AEF=∠A′EF,∠BEH=∠B′EH,即可得到结论;
(2)①由正方形A′B′C′D′的面积是4,求得A′B′=B′C′=C′D′=A′D′=2,根据线段中点的定义得到EB′=HC′=GD′=FA′=4,根据折叠的性质得BE=BE′=4,求得AB=AE+BE=6,根据正方形的面积即可得到结论;
②设正方形A′B′C′D′的边长为x,根据题意列方程即可得到结论.
解答 解:(1)∵将正方形纸片的一角折叠,使点A落在点A′处,折痕为EF,再把BE折过去与EA′重合,EH为折痕,
∴△A′EF≌△AEF,△B′EH≌△BEH,
∴AE=A′E,BE=B′E,∠AEF=∠A′EF,∠BEH=∠B′EH,
∴∠FEH=∠FEA′+∠HEB′=$\frac{1}{2}$∠AEB=90°,
故答案为:A′E,B′E,90°;
(2)①∵正方形A′B′C′D′的面积是4,
∴A′B′=B′C′=C′D′=A′D′=2,
∵点A′、B′、C′、D′恰好是B′E、C′H、D′G、A′F的中点,
∴EB′=HC′=GD′=FA′=4,
根据折叠的性质得BE=BE′=4,
∴AB=AE+BE=6,
∴正方形ABCD的面积是36;
故答案为:36;
②设正方形A′B′C′D′的边长为x,
根据题意得:2×4x-36=4(x+3+3),
解得:x=15,
∴A′B′C′D′的边长=15.
点评 本题考查了正方形的性质,折叠的性质,正方形的面积和周长的计算,线段中点的定义,熟练掌握折叠的性质是解题的关键.


科目:初中数学 来源: 题型:解答题
| 品名 | 茄子 | 豆角 |
| 批发价(元/千克) | 3.0 | 3.5 |
| 零售价(元/千克) | 4.5 | 5.2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3m2n与3nm2 | B. | $-\frac{1}{4}{x^2}{y^{c+6}}$xy2与2x2+ay3x2y2 | ||
| C. | -5ab与-5×103ab | D. | 35与-12 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com