
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:初中数学 来源:不详 题型:填空题
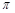 )
)
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 中,
中, ,
, ,点
,点 从
从 开始沿折线A-B-C-D以4cm/s的速度移动,点
开始沿折线A-B-C-D以4cm/s的速度移动,点 从
从 开始沿
开始沿 边以1cm/s的速度移动,如果点
边以1cm/s的速度移动,如果点 、
、 分别从
分别从 、
、 同时出发,当其中一点到达
同时出发,当其中一点到达 时,另一点也随之停止运动。设运动时间为t(s)。
时,另一点也随之停止运动。设运动时间为t(s)。 为矩形?
为矩形? 和
和 的半径都是2cm,那么t为何值时,
的半径都是2cm,那么t为何值时, 和
和 外切。
外切。
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
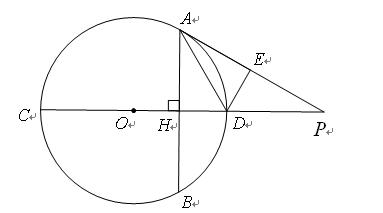
 ,OB长为半径作圆,恰好经过点A,并与BC交于点D.
,OB长为半径作圆,恰好经过点A,并与BC交于点D. ,求图中阴影部分的面积(结果保留π).
,求图中阴影部分的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
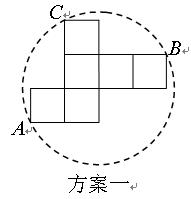
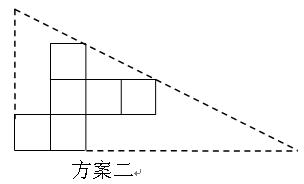

 纸片利用率=
纸片利用率= ×100%
×100% 你认为小明的这个发现是否正确,请说明理由.
你认为小明的这个发现是否正确,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com