
观察控究,完成证明和填空.
如图,四边形ABCD中,点E、F、G、H分别是边AB、BC、CD、DA的中点,顺次连接E、F、G、H,得到的四边形EFGH叫中点四边形.
(1)求证:四边形EFGH是平行四边形;
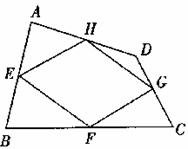
(2)如图,当四边形ABCD变成等腰梯形时,它的中点四边形是菱形,请你探究并填空:
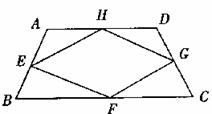
当四边形ABCD变成平行四边形时,它的中点四边形是__________;
当四边形ABCD变成矩形时,它的中点四边形是__________;
当四边形ABCD变成菱形时,它的中点四边形是__________;
当四边形ABCD变成正方形时,它的中点四边形是__________;
(3)根据以上观察探究,请你总结中点四边形的形状由原四边形的什么决定的?
 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:
为净化空气,美化环境,某市冷水滩区在许多街道和居民小区都种植上了玉兰和樟树,冷水滩区新建的某住宅区内,计划投资1.8万元种植玉兰树和樟树共80棵,已知某苗圃负责种植活以上两种树苗的价格分别为:玉兰树300元/棵,樟树200元/棵,问可种植玉兰树和樟树各多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,正六边形ABCDEF的边长为4,两顶点A、B分别在x轴和y轴上运动,则顶点D到原点O的距离的最大值和最小值的乘积为( )
A、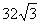 B、48 C、 32 D、
B、48 C、 32 D、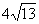
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
抛物线y=3(x-2)2+1图象上平移2个单位,再向左平移2个单位所得的解析式为 ( )
A.y=3x2+3 B.y=3x2-1 C.y=3(x-4)2+3 D. y=3(x-4)2-1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com