
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120°,将有一30度角的直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.(图中∠OMN=30°,∠NOM=90°) 
(1)将图1中的三角板绕点O逆时针旋转至图2,使OM在∠BOC的内部,且恰好平分∠BOC,问直线ON是否平分∠AOC?请说明理由;
(2)将图1中的三角板绕点O按每秒6°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,求t;
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
【答案】
(1)解:直线ON平分∠AOC;
理由:
设ON的反向延长线为OD,
∵OM平分∠BOC,
∴∠MOC=∠MOB=60°,
又∵OM⊥ON,
∴∠MON=90°,
∴∠BON=30°,
∴∠CON=120°+30°=150°,
∴∠COD=30°,
∴OD平分∠AOC,
即直线ON平分∠AOC
(2)解:由(1)可知∠BON=30°,∠DON=180°
因此ON旋转60°或240°时直线ON平分∠AOC,
由题意得,6t=60°或240°,
∴t=10或40
(3)解:∵∠MON=90°,∠AOC=60°,
∴∠AOM=90°﹣∠AON、∠NOC=60°﹣∠AON,
∴∠AOM﹣∠NOC=(90°﹣∠AON)﹣(60°﹣∠AON)=30°
【解析】(1)由角的平分线的定义和等角的余角相等求解;(2)由∠BOC=120°可得∠AOC=60°,则∠AON=30°或∠NOR=30°,即顺时针旋转300°或120°时ON平分∠AOC,据此求解;(3)因为∠MON=90°,∠AOC=60°,所以∠AOM=90°﹣∠AON、∠NOC=60°﹣∠AON,然后作差即可.
【考点精析】掌握角的平分线和余角和补角的特征是解答本题的根本,需要知道从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线;互余、互补是指两个角的数量关系,与两个角的位置无关.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
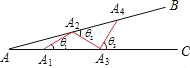
【题目】如图,设∠BAC=θ(0°<θ<90°).现把小棒依次摆放在两射线之间,并使小棒两端分别落在射线AB,AC上.从点![]() 开始,用等长的小棒依次向右摆放,其中
开始,用等长的小棒依次向右摆放,其中![]() 为第一根小棒,且
为第一根小棒,且![]() =
=![]() .
.
(1)小棒能无限摆下去吗?答: .(填“能”或“不能”)
(2)若已经摆放了3根小棒,则![]() = ,
= ,![]() = ,
= ,![]() = ;(用含
= ;(用含![]() 的式子表示)
的式子表示)
(3)若只能摆放4根小棒,求![]() 的范围.
的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在一次数学检测中,八年级甲、乙两班学生的数学成绩统计如下表:
分数 | 50 | 60 | 70 | 80 | 90 | 100 | |
人数 | 甲班 | 1 | 6 | 12 | 11 | 15 | 5 |
乙班 | 3 | 5 | 15 | 3 | 13 | 11 | |
请根据表中提供的信息回答下列问题:
(1)甲班的众数是多少分,乙班的众数是多少分,从众数看成绩较好的是哪个班?
(2)甲班的中位数是多少分,乙班的中位数是多少分,甲班成绩在中位数以上(包括中位数)的学生所占的百分比是多少;乙班成绩在中位数以上(包括中位数)的学生所占的百分比是多少,从中位数看成绩较好的是哪个班?
(3)甲班的平均成绩是多少分,乙班的平均成绩是多少分,从平均成绩看成绩较好的班是哪个班?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O为直线AB上一点,∠AOC=110°,OM平分∠AOC,∠MON=90° 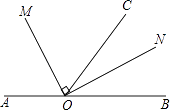
(1)求∠BOM的度数;
(2)ON是∠BOC的角平分线吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在50包型号为L的衬衫的包裹中混进了型号为M的衬衫,每包20件衬衫,每包中混入的M号衬衫数如表:
M号衬衫数 | 0 | 1 | 4 | 5 | 7 | 9 | 10 | 11 |
包数 | 7 | 3 | 10 | 15 | 5 | 4 | 3 | 3 |
根据以上数据,选择正确选项( ).
A.M号衬衫一共有47件
B.从中随机取一包,包中L号衬衫数不低于9是随机事件
C.从中随机取一包,包中L号衬衫数不超过4的概率为0.26
D.将50包衬衫混合在一起,从中随机拿出一件衬衫,恰好是M号的概率为0.252
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com