
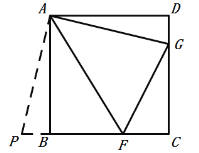
【题目】(1)如图,在正方形 ABCD 中,∠FAG=45°,请直接写出 DG,BF 与FG 的数量关系,不需要证明.
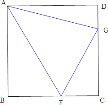
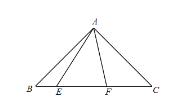
(2)如图,在 Rt△ABC 中,∠BAC=90°,AB=AC,E,F 分别是 BC 上两点,∠EAF=45°,
①写出 BE,CF,EF 之间的数量关系,并证明.
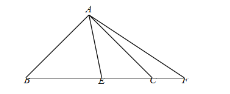
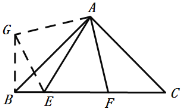
②若将(2)中的△AEF 绕点 A 旋转至如图所示的位置,上述结论是否仍然成立? 若不成立,直接写出新的结论 ,无需证明.
(3)如图,△AEF 中∠EAF=45°,AG⊥EF 于 G,且GF=2,GE=3,则 ![]() = .
= .
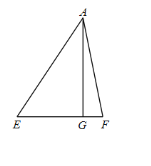
【答案】(1)FG=BF+DG;(2)①EF2=BE2+FC2,理由见解析;②仍然成立;(3)15
【解析】
(1)把△AGD绕点A逆时针旋转90°至△ABP,可使AD与AB重合,再证明△AFG≌△AFP进而得到PF=FG,即可得FG=BF+DG;
(2)①根据△AFC绕点A顺时针旋转90°得到△AGB,根据旋转的性质,可知△ACF≌△ABG得到BG=FC,AG=AF,∠C=∠ABG,∠FAC=∠GAB,根据Rt△ABC中的AB=AC得到∠GBE=90°,所以GB2+BE2=GE2,证△AGE≌△AFE,利用EF=EG得到EF2=BE2+FC2;
②将△ABE绕点A逆时针旋转使得AB与AD重合,点E的对应点是G,同上的方法证得GC2+CF2=FG2,再设法利用SAS证得△AFG≌△AFE即可求解;
(3)将△AEG沿AE对折成△AEB,将△AFG沿AF对折成△AFD,延长BE、DF相交于C,构成正方形ABCD,在Rt△EFC中,利用勾股定理求得正方形的边长,即可求得AG的长,从而求得答案.
(1)∵四边形ABCD为正方形,
∴AB=AD,∠ADC=∠ABC=90°,
∴把△AGD绕点A逆时针旋转90°至△ABP,使AD与AB重合,
∴∠BAP=∠DAG,AP= AG,
∵∠BAD=90°,∠FAG=45°,
∴∠BAF+∠DAG=45°,
∴∠PAF=∠FAG=45°,
∵∠ADC=∠ABC=90°,
∴∠FBP=180°,点F、B、P共线,
在△AFG和△AFP中,
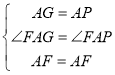 ,
,
∴△AFG≌△AFP(SAS),
∴PF=FG,
即:FG=BF+DG;
(2)①FC2+BE2=EF2,证明如下:
∵AB=AC,∠BAC=90°,
∴∠C=∠ABC=45°,
将△AFC绕点A顺时针旋转90°得到△AGB,
∴△ACF≌△ABG,
∴BG=FC,AG=AF,∠C=∠ABG=45°,∠FAC=∠GAB,
∴∠GBE=∠ABG +∠ABC =90°,
∴GB2+BE2=GE2,
又∵∠EAF=45°,
∴∠BAE+∠FAC=45°,
∴∠GAB+∠BAE=45°,
即∠GAE=45°,
在△AGE和△AFE中,
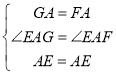 ,
,
∴△AGE≌△AFE(SAS),
∴GE=EF,
∴FC2+BE2=EF2;
②仍然成立,理由如下:
如图,将△ABE绕点A逆时针旋转使得AB与AD重合,点E的对应点为点G,
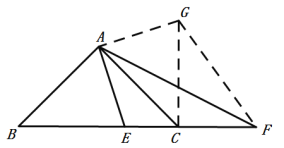
∴△ACG≌△ABE,
∴CG=BE,AG=AE,∠ACG=∠ABE=45°,∠BAE=∠CAG,
∴∠GCB=∠ACB +∠ACG =90°,即∠GCF=90°,
∴GC2+CF2=FG2,
∵∠BAE+∠EAC=∠BAC=90°,
∴∠CAG+∠EAC=90°,
又∵∠EAF=45°,
∴∠GAF=90°-∠EAF=45°,
∴∠GAF=∠EAF=45°,
在△AFG和△AFE中,
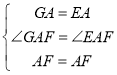 ,
,
∴△AFG≌△AFE(SAS),
∴GF=EF,
∴FC2+BE2=EF2;

(3)将△AEG沿AE对折成△AEB,将△AFG沿AF对折成△AFD,延长BE、DF相交于C,
∴△AEG![]() △AEB,△AFG
△AEB,△AFG![]() △AFD,
△AFD,
∴AB=AG=AD,BE=EG=3,DF=FG=2,∠EAG=∠EAB,∠FAG=∠FAD,∠B=∠D=90°,
∵∠EAF=45°,
∴∠EAB+∠FAD=∠EAG+∠FAG=∠EAF=45°,
∴∠BAD=90°,
∴四边形ABCD为正方形,
设AG =![]() ,则AB=BC=CD=
,则AB=BC=CD=![]() ,
,
在Rt△EFC中,EF=3+2=5,EC=BC-BE=![]() ,FC=CD-DF=
,FC=CD-DF=![]() ,
,
∴![]() ,
,
故![]() ,
,
解得:![]() (舍去),
(舍去),![]() ,
,
∴AG=6,
∴![]() .
.
故答案为:15.


科目:初中数学 来源: 题型:
【题目】完全平方公式:(a±b)2=a2±2ab+b2适当的变形,可以解决很多的数学问题.
例如:若a+b=3,ab=1,求a2+b2的值.
解:因为a+b=3,ab=1
所以(a+b)2=9,2ab=2
所以a2+b2+2ab=9,2ab=2
得a2+b2=7
根据上面的解题思路与方法,解决下列问题:
(1)若(7﹣x)(x﹣4)=1,求(7﹣x)2+(x﹣4)2的值;
(2)如图,点C是线段AB上的一点,以AC、BC为边向两边作正方形,设AB=5,两正方形的面积和S1+S2=17,求图中阴影部分面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,DE分别是AB,AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连CF
(1)求证:四边形BCFE是菱形;
(2)若CE=6,∠BEF=120°,求菱形BCFE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于二次函数y=ax2+bx+c的图象有下列命题:
①当c=0时,函数的图象经过原点;
②当c>0,且函数的图象开口向下时,方程ax2+bx+c=0必有两个不相等的实根;
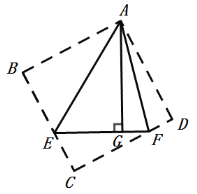
③函数图象最高点的纵坐标是![]() ;
;
④当b=0时,函数的图象关于y轴对称.
其中正确命题的个数是( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过 1 千克的,按每千克 22 元收费;超过 1 千克,超过的部分按每千克 15元收费.乙公司表示:按每千克 16 元收费,另加包装费 3 元.设小明快递物品x 千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用 y(元)与 x(千克)之间的函数关系式;
(2)当 ![]() 为何值时小明选择乙快递公司更省钱?
为何值时小明选择乙快递公司更省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学举行电脑知识竞赛,将八年级两个班参赛学生的成绩(得分均为整数)进行整理后,分成5组,绘制出如下的频数分布直方图(如图),已知图中从左到右的第一、第三、第四、第五小组的频率分别为0.30、0.15、0.10、0.05,第二组的频数是40
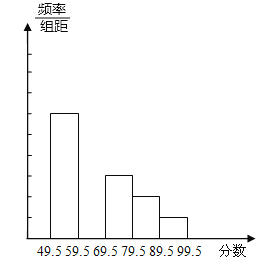
(1)求第二组的频率,并补全这个频数分布直方图;
(2)这两个班参赛的学生人数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在对Rt△OAB依次进行位似、轴对称和平移变换后得到△O′A′B′.
(1)在坐标纸上画出这几次变换相应的图形;
(2)设P(x,y)为△OAB边上任一点,依次写出这几次变换后点P对应点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,…,都是斜边在x轴上、斜边长分别为2,4,6,…的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2013的坐标为

A. (2,1006)B. (1008,0)C. ( -1006,0)D. (1,-1007)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王平同学为小明与小丽设计了一种游戏.游戏规则是:取3张数字分别是2、3、4的扑克牌,将牌洗匀后背面朝上放置在桌面上,第一次随机抽出一张牌记下数字后再按原样放回,洗匀后第二次再随机抽出一张牌记下数字,若抽出的两张牌上的数字之和为偶数,则小明胜;若两数字之和为奇数,则小丽胜.问这种游戏规则公平吗?请通过画树状图或列表说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com