
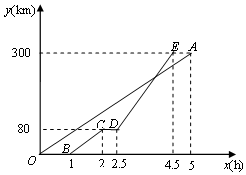
 甲、乙两地相距300km,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离甲地距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地距离y(km)与时间x(h)之间的函数关系.请根据图象,解答下列问题:
甲、乙两地相距300km,一辆货车和一辆轿车先后从甲地出发向乙地.如图,线段OA表示货车离甲地距离y(km)与时间x(h)之间的函数关系,折线BCDE表示轿车离甲地距离y(km)与时间x(h)之间的函数关系.请根据图象,解答下列问题:分析 (1)根据点C、D的横坐标,即可求出轿车在途中停留的时间;
(2)根据速度=路程÷时间,即可求出货车的平均速度;
(3)观察函数图象,找出点的坐标,利用待定系数法即可求出线段DE对应的函数解析式.
解答 解:(1)2.5-2=0.5(h).
故答案为:0.5.
(2)300÷5=60(km/h).
故答案为:60.
(3)设线段DE对应的函数解析式为y=kx+b(2.5≤x≤4.5),
将点D(2.5,80)、点E(4.5,300)代入y=kx+b,
$\left\{\begin{array}{l}80=2.5k+b\\ 300=4.5k+b\end{array}\right.$,解得:$\left\{\begin{array}{l}k=110\\ b=-195\end{array}\right.$.
∴线段DE对应的函数解析式为y=110x-195(2.5≤x≤4.5).
点评 本题考查了一次函数的应用以及待定系数法求一次函数解析式,解题的关键是:(1)利用点D的横坐标-点C的横坐标,求出停留时间;(2)根据数量关系,列式计算;(3)根据点的坐标,利用待定系数法求出线段DE的函数解析式.


科目:初中数学 来源: 题型:选择题
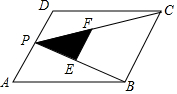 如图,P为?ABCD的边AD上的一点,E、F分别是PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2,若S=3,则S1+S2的值是( )
如图,P为?ABCD的边AD上的一点,E、F分别是PB、PC的中点,△PEF、△PDC、△PAB的面积分别为S、S1、S2,若S=3,则S1+S2的值是( )| A. | 3 | B. | 6 | C. | 12 | D. | 24 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 成绩 | 记录 | 频数 | 百分比 |
| 优秀 | 正正正正正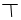 | 27 | 30% |
| 良好 | 正正正正正正正 | 36 | 40% |
| 及格 | 正正正 | 18 | 20% |
| 不及格 | 正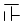 | 9 | 10% |
| 合计 | 90人 | 90 | 100% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
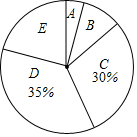 今年5月份,某校九年级学生参加了南宁市中考体育考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:
今年5月份,某校九年级学生参加了南宁市中考体育考试,为了了解该校九年级(1)班同学的中考体育情况,对全班学生的中考体育成绩进行了统计,并绘制以下不完整的频数分布表(如表)和扇形统计图(如图),根据图表中的信息解答下列问题:| 分组 | 分数段(分) | 频数 |
| A | 36≤x<41 | 3 |
| B | 41≤x<46 | n |
| C | 46≤x<51 | 18 |
| D | 51≤x<56 | m |
| E | 56≤x<61 | 17 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com