
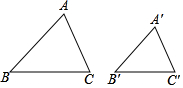
 如图,用计算机或图形计算器画△ABC和△A′B′C′,使得∠A和∠A′都等于给定的∠α,∠B和∠B′都等于给定的∠β,那么∠C和∠C′相等吗?对应边的比$\frac{AC}{A′C′}$,$\frac{AB}{A′B′}$,$\frac{BC}{B′C′}$相等吗?这样的两个三角形相似吗?
如图,用计算机或图形计算器画△ABC和△A′B′C′,使得∠A和∠A′都等于给定的∠α,∠B和∠B′都等于给定的∠β,那么∠C和∠C′相等吗?对应边的比$\frac{AC}{A′C′}$,$\frac{AB}{A′B′}$,$\frac{BC}{B′C′}$相等吗?这样的两个三角形相似吗? 互动英语系列答案
互动英语系列答案科目:初中数学 来源: 题型:选择题
 如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△EOC=1:5,则$\frac{BE}{EC}$的值为( )
如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△EOC=1:5,则$\frac{BE}{EC}$的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{5}$ | D. | $\frac{1}{25}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | ($\sqrt{a}$)2=a | B. | 若a>b(ab≠0),则$\frac{1}{a}$<$\frac{1}{b}$ | ||
| C. | |a|•|b|=|ab| | D. | 若m为整数,则(m+$\frac{1}{2}$)2+$\frac{7}{4}$是整数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com