
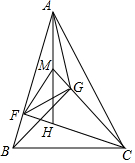
 如图,△ABC为锐角三角形,CF⊥AB于F,H为△ABC的垂心.M为AH的中点,点G在线段CM上,且CG⊥GB.
如图,△ABC为锐角三角形,CF⊥AB于F,H为△ABC的垂心.M为AH的中点,点G在线段CM上,且CG⊥GB.分析 (1)首先证明∠HCT=∠FAM=∠MFA,利用B、C、G、F四点共圆可知∠AFG=∠BCG,由此即可解决问题;
(2)由∠FMG=∠FMC,∠MFG=∠MCF,推出△MFG∽△MCF,可得$\frac{MF}{MC}$=$\frac{MG}{MF}$,推出MF2=MG•MC,由MA=MF,推出MA2=MG•MC,可得$\frac{MA}{MG}$=$\frac{MC}{MA}$,又∠AMG=∠AMC,即可证明△MAG∽△MCA,由此即可解决问题;
解答 证明:(1)如图延长AH交BC于T.
∵H是△ABC的垂心,
∴∠THC=∠HFA=90°,
∵∠THC=∠AHF,
∴∠HCT=∠FAH,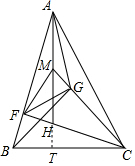
在Rt△AFH中,∵AM=MH,
∴FM=AM=MH,
∴∠FAH=∠MFA,
∴∠MFA=∠HCT,
∵BG⊥CM,
∴∠BFC=∠BGC=90°,
∴B、C、G、F四点共圆,
∴∠AFG=∠BCG,
∴∠AFM+∠MFG=∠HCT+∠MCF,
∴∠MFG=∠GCF.
(2)∵∠FMG=∠FMC,∠MFG=∠MCF,
∴△MFG∽△MCF,
∴$\frac{MF}{MC}$=$\frac{MG}{MF}$,
∴MF2=MG•MC,
∵MA=MF,
∴MA2=MG•MC,
∴$\frac{MA}{MG}$=$\frac{MC}{MA}$,∵∠AMG=∠AMC,
∴△MAG∽△MCA,
∴∠MCA=∠HAG.
点评 本题考查三角形的垂心、四点共圆、相似三角形的判定和性质等知识,解题的关键是正确寻找相似三角形解决问题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:解答题
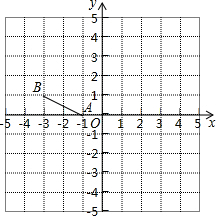 如图已知A点坐标为(-1,0),B点(-3,1).
如图已知A点坐标为(-1,0),B点(-3,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平行四边形ABCD中,点E是AD边的中点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AE}$=$\overrightarrow{b}$.
如图,在平行四边形ABCD中,点E是AD边的中点,设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AE}$=$\overrightarrow{b}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com