
����Ŀ����ͼ����![]() �У�
��![]() ��
��![]() ������
������![]() �ӵ�
�ӵ�![]() ��������
��������![]() ��ÿ��
��ÿ��![]() ����λ���ȵ��ٶ����յ�
����λ���ȵ��ٶ����յ�![]() �˶�������
�˶�������![]() ���
���![]() ��
��![]() ���غ�ʱ������
���غ�ʱ������![]() ��
��![]() ������
������![]() �ڵ�
�ڵ�![]() ����
����![]() ��������������
��������������![]() ����������
����������![]() ��
��![]() �ص�����ͼ�ε����Ϊ
�ص�����ͼ�ε����Ϊ![]() ��ƽ����λ������
��ƽ����λ������![]() �˶���ʱ��Ϊ
�˶���ʱ��Ϊ![]() ���룩��
���룩��
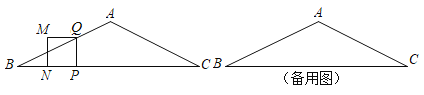
�������� ����ͼ
��1���ú�![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() �ij���
�ij���
��2��ֱ��д����![]() ��
��![]() �ڲ�ʱ
�ڲ�ʱ![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��4��ֱ��д����![]() ����
����![]() ����λ������ֱ����ʱ
����λ������ֱ����ʱ![]() ��ֵ��
��ֵ��
���𰸡���1��PQ=![]() ����2��
����2��![]() ����3����
����3����![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() ����
����![]() ʱ��
ʱ��![]() ����4��
����4��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��������
��1���������������:����Q���߶�AB��ʱ,����Q���߶�AC��ʱ;
��2���ȼ���M�ڱ�AB��ʱt��ֵ,���ݵ�M�ڡ�ABC�ڲ�ʱ�����߽�㼴�ɽ��;
��3�����������:
��0��t��1ʱ,������PQMN���ABC�ص�����ͼ�����ı���DNPQ,
����1��t��![]() ʱ,������PQMN���ABC�ص�����ͼ���������ODNPQ,
ʱ,������PQMN���ABC�ص�����ͼ���������ODNPQ,
����![]() ��t��2ʱ,������PQMN���ABC�ص�����ͼ����������MNPQ,
��t��2ʱ,������PQMN���ABC�ص�����ͼ����������MNPQ,
�ֱ�����������;
��4����M���ڡ�ABC����λ������ֱ����ʱ,�����������,��ͼ�ɽ��
��:��1���������:BP��2t,
��ͼ1,��A��AD��BC��D,
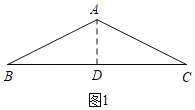
��AB��AC��![]() ,BC��4,
,BC��4,
��BD��CD��![]() BC��2��
BC��2��
��AD��![]() ,
,
��tan��B��![]() ��
��![]() ,
,
���������:
������Q���߶�AB��ʱ,��0��t��1ʱ,��ͼ2,
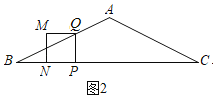
��tan��B��![]() ,
,
��PQ��t;
������Q���߶�AC��ʱ,��1��t��2ʱ,��ͼ3,
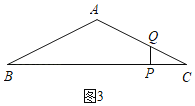
��tan��C��tan��B��![]() ��
��![]() ,
,
��PQ��![]() PC��
PC��![]() ��2��t;
��2��t;
��2����M�ڱ�AB��ʱ,��ͼ4,
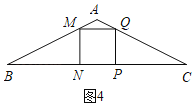
�ɣ�1��֪:MN��PQ��2��t��PN,
tan��B��![]() ��
��![]() ,
,
��BN��2MN,
��BP��BN+PN,
��2t��3MN��3��2��t��,
t��![]() ,
,
���M�ڡ�ABC�ڲ�ʱt��ȡֵ��Χ��![]() ��t��2;
��t��2;
��3�����������:
��0��t��1ʱ,��ͼ5,������PQMN���ABC�ص�����ͼ�����ı���DNPQ,
BP��2t,PQ��PN��MD��t,
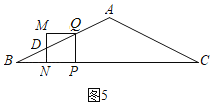
��BN��2t��t��t,
��DN��![]() t��DM,
t��DM,
��S��S������MNPQ��S��MDQ��![]() ;
;
����1��t��![]() ʱ,��ͼ6,������PQMN���ABC�ص�����ͼ���������ODNPQ,
ʱ,��ͼ6,������PQMN���ABC�ص�����ͼ���������ODNPQ,
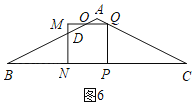
��PQ��PN��MN��2��t,
��BN��BP��PN��2t����2��t����3t��2,
��tan��B��![]() ,DN��
,DN��![]() BN��
BN��![]() ,
,
��DM��MN��DN��2��t��![]() ��3��
��3��![]() t,
t,
��tan��MOD��tan��B��![]() ��
��![]() ,
,
��OM��2MD,
��S��S������MNPQ��S��MDO����2��t��2��![]() ����2��t��2��
����2��t��2��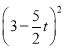 ����
����![]() +11t��5;
+11t��5;
����![]() ��t��2ʱ,��ͼ7,������PQMN���ABC�ص�����ͼ����������MNPQ,
��t��2ʱ,��ͼ7,������PQMN���ABC�ص�����ͼ����������MNPQ,
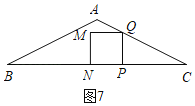
S��PQ2����2��t��2��t2��4t+4;
����,S��t֮��ĺ�����ϵʽΪ:S��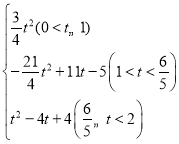 ��
��
��4�������������:
����ͼ8,M����λ��MQ��,��Q��AB���е�,BQ��![]() ,
,
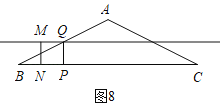
��BP��1��2t,
t��![]() ;
;
����ͼ9,M����λ��MT��,��T��BC���е�,BT��2,

��MT��AC,
���C����BTM,
��tan��BTM��![]() ,
,
��NT��BP,
��BP+TN��BT��PN,
��2t+2t��2��t,t��![]() ;
;
����ͼ10,M����λ��MQ��,
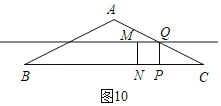
��Q��AC���е�,
ͬ����CP��1��4��2t,t��![]() ,
,
����ͼ11,M����λ��MT��,T��BC���е�,
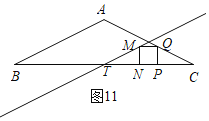
CP��TN��4��2t,PQ��PN��2��t,
��CT��TN+PN+PC,
��2��2��4��2t��+2��t,
t��![]() ;
;
����,t��ֵ��![]() ���
���![]() ���
���![]() ���
���![]() �룮
�룮


 ����ȫ���ִʾ��ƪ��ϵ�д�
����ȫ���ִʾ��ƪ��ϵ�д� �����߿����ϵ�д�
�����߿����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
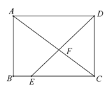
����Ŀ����ͼ���ھ��� ABCD �У�E �DZ� BC ����һ�㣬���� DE ���Խ��� AC �ڵ� F���� AB=6��AD=8��BE=2���� AF �ij�Ϊ _________________ ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1,��ƽ��ֱ������ϵ��,ֱ��![]() ��������
��������![]() ����
����![]() ���㣬����
���㣬����![]() ,
,![]() .����������
.����������![]() �ύ�ڵ�
�ύ�ڵ�![]() ,��
,��![]() �ύ����һ��
�ύ����һ��![]() .
.

(1)��![]() ��ֵ���������ߵĽ���ʽ;
��ֵ���������ߵĽ���ʽ;
(2)��ͼ2.����![]() Ϊ�߶�
Ϊ�߶�![]() �ϵ�һ����(����
�ϵ�һ����(����![]() �غ�).�ֱ���
�غ�).�ֱ���![]() ��
��![]() Ϊб��,��ֱ��
Ϊб��,��ֱ��![]() ��ͬ��������ֱ����
��ͬ��������ֱ����![]() �͵���ֱ����
�͵���ֱ����![]() ,����
,����![]() ,��ȷ����
,��ȷ����![]() ������ʱ
������ʱ![]() �������.
�������.
(3)��ͼ3.����![]() ��
��![]() ,���߶�
,���߶�![]() ���Ƿ���ڵ�
���Ƿ���ڵ�![]() ,ʹ����
,ʹ����![]() Ϊ���������������
Ϊ���������������![]() ����,������,��ֱ��д����
����,������,��ֱ��д����![]() ������;��������,��˵������.
������;��������,��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
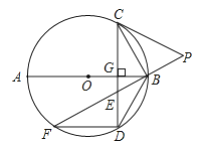
����Ŀ����ͼ��![]() Ϊ
Ϊ![]() ��ֱ����
��ֱ����![]() �ڵ�
�ڵ�![]() ��
��![]() ��
��![]() ��һ�㣬��
��һ�㣬��![]() ���ӳ�
���ӳ�![]() ����
����![]() ������
������![]() ��ʹ
��ʹ![]() ���ӳ�
���ӳ�![]() ��
��![]() ���ڵ�
���ڵ�![]() ������
������![]() ��
��![]() ��
��
��1������![]() ����֤��
����֤��![]() ��
��
��2����֤��![]() ��
��![]() �����ߣ�
�����ߣ�
��3����![]() ��
��![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������
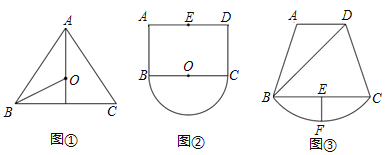
��1����ͼ�٣��ڡ�ABC�У�AB��AC��10��BC��12����O�ǡ�ABC�����Բ��Բ�ģ���OB�ij�Ϊ�� ��
����̽��
��2����ͼ�ڣ���֪����ABCD��AB��4��AD��6����EΪAD���е㣬��BCΪֱ������ԲO����PΪ��ԲO��һ���㣬��E��P֮��������룻
������
��3��ij����һ����ͼ����ʾ�Ĺ����������ı���ABCD����CB�������Ե��ӻ�������ɵģ���������Ҫ�����D��![]() �ϵ�һ��P��һ����ֱ��С·DP����֪AD��BC����ADB��45����BD��120
�ϵ�һ��P��һ����ֱ��С·DP����֪AD��BC����ADB��45����BD��120![]() �ף�BC��160�ף�����BC���е�E��EF��BC��
�ף�BC��160�ף�����BC���е�E��EF��BC��![]() �ڵ�F���ֲ��EF��40�ף���С·ƽ��ÿ����Ҫ40Ԫ��С·���Ȳ��ƣ����������������أ��������������Ϣ�����������˼���������С·���Ҫ���Ѷ���Ԫ��
�ڵ�F���ֲ��EF��40�ף���С·ƽ��ÿ����Ҫ40Ԫ��С·���Ȳ��ƣ����������������أ��������������Ϣ�����������˼���������С·���Ҫ���Ѷ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ռ��ϵ����ӳ�˷��������������ͼ������ǰ���ݶ���������ʱ�����ռ��ϵ��=L����H��H1��������LΪ¥��ˮƽ���룬HΪ�ϲ�¥���߶ȣ�H1Ϊ����¥���ײ㴰̨������߶ȣ�
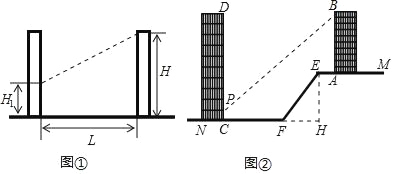
��ͼ�ڣ�ɽ��EF������EF��Ϊ15m���¶�Ϊi=1��0.75��ɽ�¶���ƽ��EM����һ��Ϊ22.5m��¥��AB���ײ�A��E��ľ���Ϊ4m��
��1����ɽ��EF��ˮƽ����FH��
��2������AB¥������ɽ�ŵ�ƽ��FN�Ͻ�һ¥��CD����֪��¥�ײ㴰̨P��������C���ĸ߶�Ϊ0.9m��Ҫʹ��¥�����ռ��ϵ��������1.25���ײ�C��F�����ٶ�Զ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
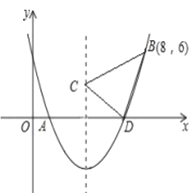
����Ŀ����ͼ�����κ���![]() ��ͼ��
��ͼ��![]() ����
����![]() ���㣬������
���㣬������![]() �㣬��֪
�㣬��֪![]() ��������
��������![]() ��
��![]() ��������
��������![]() ��
��
��1������κ����Ľ���ʽ��
��2������ͼ��Ķ������꼰![]() ������ꣻ
������ꣻ
��3�����κ����ĶԳ������Ƿ����һ��![]() ��ʹ��
��ʹ��![]() ���ܳ���С����
���ܳ���С����![]() ����ڣ����
����ڣ����![]() ������꣬��
������꣬��![]() �㲻���ڣ���˵�����ɣ�
�㲻���ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾�ƻ�����2̨���������ֻ���ʹ���������̭��������һ����������ڹ�������ʱ�����Զ�������������Ϊ������ÿ��200Ԫ���ڻ���ʹ���ڼ䣬������������ٹ�����ÿ��500Ԫ�����������������࣬ÿ����![]() Ԫ��
Ԫ��![]() �����գ���������ڹ������ʱӦͬʱ�������������Ϊ���Ѽ���������100̨���ֻ���������ʹ�����ڸ�����������������õ�����Ƶ���ֲ�ֱ��ͼ��
�����գ���������ڹ������ʱӦͬʱ�������������Ϊ���Ѽ���������100̨���ֻ���������ʹ�����ڸ�����������������õ�����Ƶ���ֲ�ֱ��ͼ��
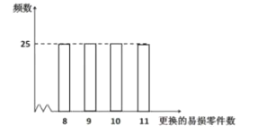
��![]() ��ʾ2̨���������ڹ�������������������
��ʾ2̨���������ڹ�������������������![]() ��ʾ����2̨������ͬʱ����������������
��ʾ����2̨������ͬʱ����������������
��1����100̨����Ϊ�����������û���״ͼ���б��ķ�������![]() ������19�ĸ��ʣ�
������19�ĸ��ʣ�
��2������100̨�����ڹ������������������õ�ƽ����Ϊ�������ݣ���![]() ��
��![]() ֮��ѡ��һ����
֮��ѡ��һ����![]() Ϊ��ֵʱ��ѡ
Ϊ��ֵʱ��ѡ![]() �Ƚϻ��㣿
�Ƚϻ��㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������OABC��һ������O��ƽ��ֱ������ϵ��ԭ�㣬����A��C�ֱ���y���x���ϣ�PΪ��OC�ϵ�һ�����㣬��PQ��BP��PQ=BP������P�ӵ�C�˶�����Oʱ����֪��Qʼ����ij����ͼ�����˶������亯��ͼ���ǣ� ��
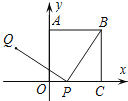
A.�߶�B.Բ��
C.˫���ߵ�һ����D.�����ߵ�һ����
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com