
分析 (1)先整理,再配方,再开方,即可得出一元一次方程,求出方程的解即可.
(2)根据待定系数法求得解析式,然后求出函数与x轴的交点和函数的最小值,即可求得函数y的取值范围.
解答 解:(1)(x+1)2=4x;
整理得:x2-2x+1=0,
(x-1)2=0,
x-1=±0,
x1=x2=1;
(2)将点P(-2,5)代入y=x2+bx-3得,4-2b-3=5,
解得b=-2,
∴二次函数的解析式为y=x2-2x-3,
当y=0时,x2-2x-3=0,
(x+1)(x-3)=0,
x1=-1,x2=3,
其对称轴为x=-$\frac{-2}{2×1}$=1,最小值为y=-4,
∴1<x≤3时,-4<y≤0.
点评 本题考查了解一元二次方程的应用,二次函数的性质和二次函数图象上点的坐标特征,要熟悉函数和方程的关系,培养学生的计算能力.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:解答题
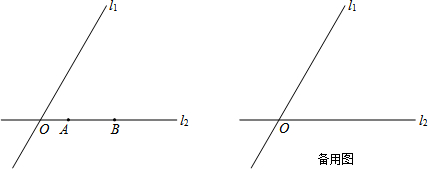
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
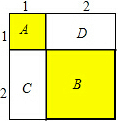 我们初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释.例如:平方差公式、完全平方公式.
我们初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释.例如:平方差公式、完全平方公式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com