
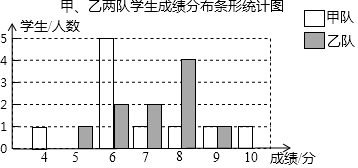
| 平均分 | 中位数 | 众数 | 方差 | 合格率 | 优秀率 | |
| 甲队 | a | 6 | c | 2.76 | 90% | 20% |
| 乙队 | 7.2 | b | 8 | 1.36 | 80% | 10% |
分析 (1)利用条形统计图,根据平均数、中位数和众数的定义求解;
(2)利用中位数的意义进行判断;
(3)从平均数、方差或众数的意义进行说明;
(4)画树状图(甲队的优秀学生用A、A表示,乙队的优秀学生用B表示)展示所有6种等可能的结果数,再找出恰好同时选中的两人均为甲队学生的结果数,然后根据概率公式求解.
解答 解:(1)a=$\frac{1}{10}$×(4×1+6×5+7×1+8×1+9×1+10×1)=6.8,
b=$\frac{7+8}{2}$=7.5,
c为6;
(2)因为甲的中位数为6,而乙的中位数为7,如果成绩属于中等偏上的位置,则应该为甲组;
(3)乙队的平均分高于甲队的平均分;
乙的方差小于甲队的方差,乙队的成绩比较稳定;
(4)画树状图为:(甲队的优秀学生用A、A表示,乙队的优秀学生用B表示)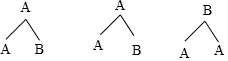
共有6种等可能的结果数,其中恰好同时选中的两人均为甲队学生的结果数为2,
所以恰好同时选中的两人均为甲队学生的概率=$\frac{2}{6}$=$\frac{1}{3}$.
故答案为6.8,7,6;甲;$\frac{1}{3}$.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式求事件A或B的概率.也考查了统计的有关概念.


科目:初中数学 来源: 题型:填空题
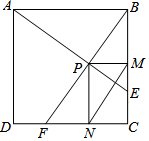 如图,在边长为1的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),过点P作PM∥CD交BC于M点,PN∥BC交CD于N点,连接MN,在运动过程中,
如图,在边长为1的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),过点P作PM∥CD交BC于M点,PN∥BC交CD于N点,连接MN,在运动过程中,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
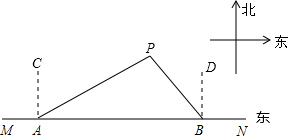 如图,船A、B在东西方向的海岸线MN上,均收到已搁浅的船P的求救信号,已知船P在船A的北偏东60°方向上,在船B的北偏西45°方向上,AB=30海里.
如图,船A、B在东西方向的海岸线MN上,均收到已搁浅的船P的求救信号,已知船P在船A的北偏东60°方向上,在船B的北偏西45°方向上,AB=30海里.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
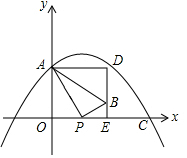 在如图所示的平面直角坐标系中,抛物线y=-$\frac{1}{6}$x2+bx+c过点A(0,4)和C(8,0),点P(t,0)是线段OC上的动点,PB⊥PA,且PB=$\frac{1}{2}$PA,过点B作x轴的垂线,过点A作y轴的垂线,两直线相交于点D;
在如图所示的平面直角坐标系中,抛物线y=-$\frac{1}{6}$x2+bx+c过点A(0,4)和C(8,0),点P(t,0)是线段OC上的动点,PB⊥PA,且PB=$\frac{1}{2}$PA,过点B作x轴的垂线,过点A作y轴的垂线,两直线相交于点D;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
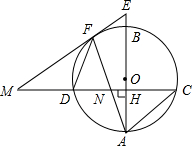 如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,与AC平行的圆O的一条切线交CD的延长线于点M,交AB的延长线于点E,切点为F,连接AF交CD于点N.
如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,与AC平行的圆O的一条切线交CD的延长线于点M,交AB的延长线于点E,切点为F,连接AF交CD于点N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com