
����Ŀ�����о�̩�ǹ�˾����![]() �����������ס������ֲ�Ʒ��ÿ��ÿ������
�����������ס������ֲ�Ʒ��ÿ��ÿ������![]() ���ײ�Ʒ��
���ײ�Ʒ��![]() ���Ҳ�Ʒ.�����г������ã��ײ�Ʒÿ���ɻ���
���Ҳ�Ʒ.�����г������ã��ײ�Ʒÿ���ɻ���![]() Ԫ���Ҳ�Ʒÿ���ɻ���
Ԫ���Ҳ�Ʒÿ���ɻ���![]() Ԫ.��ʵ�������У������Ҳ�Ʒ��Ҫ����֧��һ���ķ��ã��������㣬ÿ����
Ԫ.��ʵ�������У������Ҳ�Ʒ��Ҫ����֧��һ���ķ��ã��������㣬ÿ����![]() ���Ҳ�Ʒ������ÿ���Ҳ�Ʒƽ��ݶ������
���Ҳ�Ʒ������ÿ���Ҳ�Ʒƽ��ݶ������![]() Ԫ����ÿ�찲��
Ԫ����ÿ�찲��![]() �������Ҳ�Ʒ.
�������Ҳ�Ʒ.
(1)������Ϣ�����
��Ʒ���� | ÿ�칤����(��) | ÿ�����(��) | ÿ����Ʒ�ɻ�����(Ԫ) |
�� |
| ||
�� |
|
|
(2)��ÿ�������ײ�Ʒ�ɻ�õ�����������Ҳ�Ʒ�ɻ�õ������![]() Ԫ�����ʣ�����ҵÿ�������ס��Ҳ�Ʒ�ɻ���������Ƕ���Ԫ?
Ԫ�����ʣ�����ҵÿ�������ס��Ҳ�Ʒ�ɻ���������Ƕ���Ԫ?
���𰸡�(1) ![]() ��
��![]() ��
��![]() ��(2)����ҵÿ�������ס��Ҳ�Ʒ�ɻ����������
��(2)����ҵÿ�������ס��Ҳ�Ʒ�ɻ����������![]() Ԫ.
Ԫ.
��������
��1����ÿ�찲��x�������Ҳ�Ʒ����ÿ�찲�ţ�65-x���������ײ�Ʒ��ÿ�������x���Ҳ�Ʒ��ÿ��������Ϊ��120-2x��Ԫ��ÿ�������2��65-x�����ײ�Ʒ�����ʵý⣻
��2����������=ÿ����Ʒ�������������������ÿ�������ײ�Ʒ�ɻ�õ�����������Ҳ�Ʒ�ɻ�õ������650Ԫ�����ɵó�����x��һԪ���η��̣���֮ȡ���Сֵ���ɵó����ۣ�
�⣺��1����ÿ�찲��x�������Ҳ�Ʒ����ÿ�찲�ţ�65-x���������ײ�Ʒ��ÿ�������x���Ҳ�Ʒ��ÿ��������Ϊ��120-2x��Ԫ��ÿ�������2��65-x�����ײ�Ʒ��
�ʴ�Ϊ��![]() ��
��![]() ��
��![]() ��
��
��2�������⣬�ã�15��2��65-x��-��120-2x��x=650��
�������ã�x2-75x+650=0��
��ã�x1=10��x2=65���������⣬��ȥ����
��15��2��65-x��+��120-2x��x=2650��
�𣺸���ҵÿ�������ס��Ҳ�Ʒ�ɻ����������2650Ԫ��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������A��B�����Ӧ���������ֱ�Ϊ10��15����P�ӵ�A��������ÿ��1����λ���ȵ��ٶ��������������˶�����Qͬʱ��ԭ��O��������ÿ��2����λ���ȵ��ٶ��������������˶������˶�ʱ��Ϊt�룮
![]()
(1)��0��t��5ʱ���ú�t��ʽ����գ�
BP��_______��AQ��_______��
(2)��t��2ʱ����PQ��ֵ��
(3)��PQ��![]() ABʱ����t��ֵ��
ABʱ����t��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ͨ���۵�������ֽƬ�õ��ȱ������εIJ���ȡһ�������ε�ֽƬ�����۵�����������������£�
��һ������ͼ���Ȱ�������ABCD���ۣ��ۺ�ΪMN��
�ڶ�������E���߶�MD�ϣ�����ECD��EC���ۣ���Dǡ������MN�ϣ���Ϊ��P������BP�ɵá�BCP�ǵȱ�������
���⣺���۵������У����Եõ�PB=PC��������________________________.
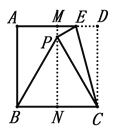
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������x��һԪ���η���ax2+bx��1��0��a��0����һ��Ϊx��2019����һԪ���η���a��x��1��2+b��x��1����1����һ��Ϊ��������
A.![]() B.2020C.2019D.2018
B.2020C.2019D.2018
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ˮ��������������A�е�һ��ˮ�������������ۣ��л������������䷽ʽ����������е���ľ�Ϊ200Ԫ��ʱ��������Ҫ�ο��������£�
���乤�� | ;��ƽ���ٶȣ�ǧ�ף�ʱ�� | �˷ѣ�Ԫ��ǧ�ף� | װж���ã�Ԫ�� |
�� | 100 | 15 | 2000 |
���� | 80 | 20 | 900 |
(1)�����������֧�����ñȻ��ö�1100Ԫ����֪��������A��֮���·���Ƕ���ǧ���������з��̽����
(2)���A����ij��֮��ľ���ΪSǧ�ף���֪������������·�ϵ����ʱ��ֱ�Ϊ2Сʱ��3.1Сʱ��������ij��ˮ���������ŵľ�����Ҫ������ˮ����A�������������ۡ��㽫ѡ���������䷽ʽ�ȽϺ����أ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
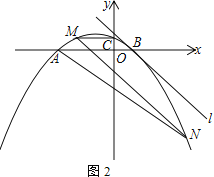
����Ŀ����֪��������y��a(x��m)(x��3m)��a��0��m��0����x�ύ��A��B���㣨��A�ڵ�B����ߣ�����y�ύ�ڵ�C��ֱ��l��y��kx��b������B���������������Ψһ�����㣬ƽ��ֱ��l����������M��N���㣨��M��N�ֱ�λ��x���Ϸ����·���
(1) ��![]() ��C(0��
��C(0��![]() )
)
�� ��������ߵĽ���ʽ
�� ��ͼ1������AM��AN����֤����MAB����NAB
(2) ��ͼ2������MC����MC��x�ᣬ��![]() ��ֵ
��ֵ

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=AC��DΪBC�е㣬AE��BD����AE=BD.
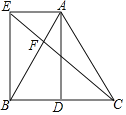
��1����֤���ı���AEBD�Ǿ��Σ�
��2������CE��AB�ڵ�F����BE=2![]() ��AE=2����EF�ij���
��AE=2����EF�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ѧ���ϣ���ʦ��ʾ������һ����Ŀ:����![]() ʱ�������ʽ
ʱ�������ʽ![]() ��ֵ���������������ź�ͬѧָ��:��
��ֵ���������������ź�ͬѧָ��:��![]() �Ƕ����������ʦ�����ۺ�һ����Ϊ����˵������ȷ�ģ���ʦ��ʱ������ͬѧ�Ƕ��ź�ͬѧ��������Լ��ļ���Ͷȥ�����͵�Ŀ�⣮
�Ƕ����������ʦ�����ۺ�һ����Ϊ����˵������ȷ�ģ���ʦ��ʱ������ͬѧ�Ƕ��ź�ͬѧ��������Լ��ļ���Ͷȥ�����͵�Ŀ�⣮
��1������˵����ȷ�����ɣ�
��2���ܴ���������ʦ�ֳ�ʾ��һ����Ŀ,������![]() ȡ�κ�ֵ������ʽ
ȡ�κ�ֵ������ʽ![]() ��ֵ�����䣬��ϵ��
��ֵ�����䣬��ϵ��![]() ��
��![]() ��ֵ����������������⣮
��ֵ����������������⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() �У�
��![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() �ֱ�
�ֱ�![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ������
������![]() ����
����![]() .
.
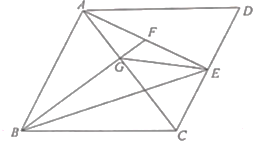
��1����![]() ����
����![]() �����.
�����.
��2����֤��![]() .
.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com