
| A.40 | B.30 | C.20 | D.10 |




科目:初中数学 来源:不详 题型:填空题

 中,
中, .如图所示,折叠纸片,使点
.如图所示,折叠纸片,使点 落在
落在 边上的
边上的 处,折痕为
处,折痕为 .当点
.当点 在
在 边上移动时,折痕的端点
边上移动时,折痕的端点 也随之移动.若限定点
也随之移动.若限定点 分别在
分别在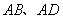 边上移动,则点
边上移动,则点 在
在 边上距B点可移动的最短距离为 .
边上距B点可移动的最短距离为 .查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

| A.等腰梯形 | B.矩形 | C.菱形 | D.正方形 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 .
.
 中选择两个条件________(用序号表示,只填一种情况),使得
中选择两个条件________(用序号表示,只填一种情况),使得 ,并加以证明.
,并加以证明.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ,求证:四边形AECF是菱形.
,求证:四边形AECF是菱形.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 的边长为2, 将长为2的线段
的边长为2, 将长为2的线段 的两端放在正方形相邻的
的两端放在正方形相邻的 从点
从点 出发,沿图中所示方向按
出发,沿图中所示方向按 滑动到点
滑动到点
 从点
从点 出发,沿图中所示方向按
出发,沿图中所示方向按 滑动到点
滑动到点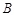 为止,那
为止,那 的中点
的中点 所经过的路线围成的图形的面积为
所经过的路线围成的图形的面积为 A.4-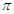 | B. |
| C.2 | D.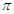 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com