
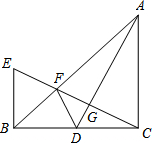
 如图,在△ABC中,∠BCA=90°,CA=CB,AD为BC边上的中线,CG⊥AD于G,交AB于F,过点B作BC的垂线交CG于E.现有下列结论:①△ADC≌△CEB;②DF=CD;③∠ADC=∠BDF;④F为EG中点.其中结论正确的为( )
如图,在△ABC中,∠BCA=90°,CA=CB,AD为BC边上的中线,CG⊥AD于G,交AB于F,过点B作BC的垂线交CG于E.现有下列结论:①△ADC≌△CEB;②DF=CD;③∠ADC=∠BDF;④F为EG中点.其中结论正确的为( )| A. | ①② | B. | ①②③ | C. | ①③ | D. | ①③④ |
分析 ①由条件可知∠ECD+∠ADC=∠E+∠ECD=90°,可得到∠E=∠ADC,再结合条件可证明△ADC≌△CEB;②AD为BC边上的中线,得到BD=CD,得到∠AFB≠90°,求得DF≠CD,③BE=CD=BD,结合条件可证明△BEF≌△BDF,则有∠E=∠BDF=∠ADC,可得结论;④由③可得EF=DF,而DF>FG,故F不可能为EG中点.
解答 解:∵∠BCA=90°,CG⊥AD,
∴∠ECD+∠ADC=∠E+∠ECD=90°,
∴∠E=∠ADC,
∵BE⊥BC,
∴∠EBC=∠ACD,
在△ADC和△CEB中$\left\{\begin{array}{l}{∠ACD=∠CBE}\\{∠DAC=∠E}\\{AC=BC}\end{array}\right.$
∴△ADC≌△CEB(AAS),
∴①正确;
∵AD为BC边上的中线,
∴BD=CD,
∵AG⊥CE,
∴∠AFB≠90°,
∴DF≠$\frac{1}{2}$CB,
∴DF≠CD,
∴②不正确;
∵△ADC≌△CEB,且D为BC中点,
∴BE=CD=BD,
∵AC=BC,∠ACB=90°,
∴∠DBF=∠EBF=45°,
在△BEF和△BDF中$\left\{\begin{array}{l}{BE=BD}\\{∠DBF=∠EBF}\\{BF=BF}\end{array}\right.$
∴△BEF≌△BDF(SAS),
∴∠E=∠BDF,又∠E=∠ADC,
∴∠ADC=∠BDF,
∴③正确;
∵△BEF≌△BDF,
∴EF=DF,
在R△DFG中,DF>FG,
∴EF>FG,
∴F不是EG的中点,
∴④不正确;
综上可知正确的有①③共两个,
故选C.
点评 本题主要考查全等三角形的判定和性质,掌握全等三角形的判定方法SSS、SAS、ASA、AAS和HL是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3a-42 | B. | 3a+42 | C. | 4a-32 | D. | 3a+32 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
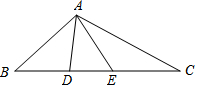 如图,△ABC的两边AB和AC的垂直平分线分别交BC于D,E,若∠BAC+∠DAE=150°,则∠BAC的度数是( )
如图,△ABC的两边AB和AC的垂直平分线分别交BC于D,E,若∠BAC+∠DAE=150°,则∠BAC的度数是( )| A. | 105° | B. | 110° | C. | 115° | D. | 120° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 遗爱湖公园的亲水平台修建了许多台阶(如图所示),春季湖水上涨后有一部分在水下.如果点C的坐标为(-1,1),D点的坐标为(0,2).(点C、D分别在第3、4级)
遗爱湖公园的亲水平台修建了许多台阶(如图所示),春季湖水上涨后有一部分在水下.如果点C的坐标为(-1,1),D点的坐标为(0,2).(点C、D分别在第3、4级)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com