练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    （1）如图，点C与建筑物AB底部B的水平距离BC=15米，从点A测得点C的俯角α=60°，求建筑物AB的高．（结果保留根号）
    （2）为了测量建筑物AB的高度，若选择在点C测点A的仰角，测角器的高度为h米，请画出测量AB高度的示意图（标上适当的字母）．
    （1）由俯角定义与平行线的性质可得，
    ∠ACB=∠α=60°，AB=BC×tan60°=15
    		3
    ．

    （2）示意图如右图．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：不详 题型：解答题

    如图，在Rt△ABC中，∠C=90°，cos∠CAB=
    4
    5
    ，AC=8，延长CB到D使得BD=AB，连接AD，求AD的长．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    如图，小敏、小亮从A，B两地观测空中C处一个气球，分别测得仰角为30°和60°，A，B两地相距100m．当气球沿与BA平行地飘移10秒后到达C′处时，在A处测得气球的仰角为45°．
    （1）求气球的高度（结果精确到0.1m）；
    （2）求气球飘移的平均速度（结果保留3个有效数字）．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

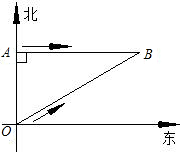    人民海关缉私巡逻艇在东海海域执行巡逻任务时，发现在其所处位置O点的正北方向10海里处的A点有一涉嫌走私船只，正以24海里/小时的速度向正东方向航行．为迅速实施检查，巡逻艇调整好航向，以26海里/小时的速度追赶，在涉嫌船只不改变航向和航速的前提下，问：
    （1）需要几小时才能追上（点B为追上时的位置）？
    （2）确定巡逻艇的追赶方向．（精确到0.1°）
    参考数据：
    sin66.8°≈0.9191；cos66.8°≈0.393
    sin67.4°≈0.9231；cos67.4°≈0.3846
    sin68.4°≈0.9298；cos68.4°≈0.3681
    sin70.6°≈0.9432；cos70.6°≈0.3322．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：填空题

    如图，将一块斜边长为12cm，∠B=60°的直角三角板ABC，绕点C沿逆时针方向旋转90°至△A′B′C′的位置，再沿CB向右平移，使点B′刚好落在斜边AB上，那么此三角板向右平移的距离是______cm．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    如图所示，当小华站立在镜子EF前A处时，他看自己的脚在镜中的像的俯角为45°．若小华向后退0.5米到B处，这时他看自己的脚在镜中的像的俯角为30°．求小华的眼睛到地面的距离．（结果精确到0.1米，参考数据：
    		3
    ≈1.73）

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    （A）某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，如图是水平放置的破裂管道有水部分的截面．
    （1）请你补全这个输水管道的圆形截面；（用圆规、直尺作图，不写作法，但要保留作图痕迹）
    （2）若这个输水管道有水部分的水面宽AB=16cm，水面最深地方的高度为4cm，求这个圆形截面的半径．
    （B）在一次实践活动中，某课题学习小组用测倾器、皮尺测量旗杆的高度，他们设计了如下方案（如图①所示）：
    （1）在测点A处安置测倾器，测得旗杆顶部M的仰角∠MCE=α；
    （2）量出测点A到旗杆底部N的水平距离AN=m；
    （3）量出测倾器的高度AC=h．
    根据上述测量数据，即可求出旗杆的高度MN．
    如果测量工具不变，请仿照上述过程，设计一个测量某小山高度（如图②）的方案：
    （1）在图②中，画出你测量小山高度MN的示意图（标上适当字母）；
    （2）写出你设计的方案．

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    某校组织学生到涪江河某段测量两岸的距离，采用了两种方案收集数据．
    方案一：如图，从C点找准对岸一参照点D，使CD垂直于河岸线l，沿河岸行走至E点，测出CE的长度后，再用电子测角器测出CE与ED的夹角α；
    方案二：如图，先从河岸上选一点A，测出A到河面的距离h．再用电子测角器测出A点到对岸河面的俯角β．

    （1）学生们选用不同的位置测量后得出以下数据，请通过计算填写下表：（精确到0.1米）
    方案一：
    测量次数123
    EC（单位：米）100150200
    α76°33′71°35′65°25′
    计算得出河宽
    （单位：米）
    方案二：
    测量次数123
    EC（单位：米）14.413.812.5
    β1°24′2°16′1°56′
    计算得出河宽
    （单位：米）
    （参考数据：tan1°24′=0.0244、tan2°16′=0.0396、tan1°56′=0.0338、tan76°33′=4.1814、tan71°35′=3.0032、tan65°25′=2.1859）
    （2）由（1）表中数据计算：
    方案一中河两岸平均宽为______米；
    方案二中河两岸平均宽为______米；
    （3）判断河两岸宽大约为______米；（从下面三个答案中选取，填入序号）
    ①390～420②420～450③350～480
    （4）求出方案一的方差S12和方案二的方差S22，判断用哪种方案测量的误差较小．（精确到1）

    查看答案和解析>>

    科目：初中数学 来源：不详 题型：解答题

    由下列条件解题：在Rt△ABC中，∠C=90°：
    （1）已知a=4，b=8，求c．
    （2）已知b=10，∠B=60°，求a，c．
    （3）已知c=20，∠A=60°，求a，b．

    查看答案和解析>>

    同步练习册答案