①②③
分析:连接AE,得到BE=CE,再由BC=2AD,可得出AD=BE=CE,根据平行四边形的判定推出四边形ABED与四边形AECD都为平行四边形,再由∠BCD=90°得出四边形AECD为矩形,得出AE垂直平分BC,推出AB=AC,即可判断①;由EF为△ABC的中位线,利用中位线定理得到EF∥AC,进而得到四边形AFEM为平行四边形,求出AF=EF,可得出四边形AFEM为菱形,即可判断②;过F作FN⊥BC,得出FN∥AE,得出FN为△ABE的中位线,FN为DC的一半,再由BE=AD,根据三角形的面积公式求出,即可判断③.
解答:解答:连接AE,

∵E为BC的中点,
∴BE=CE=

BC,
又∵BC=2AD,
∴AD=BE=EC,
又∵AD∥BC,
∴四边形ABED为平行四边形,四边形AECD为平行四边形,
又∵∠DCB=90°,
∴四边形AECD为矩形,
∴∠AEC=90°,
即AE⊥BC,
∴AE垂直平分BC,
∴AB=AC,即△ABC为等腰三角形,∴①正确;
∵E为BC的中点,F为AB的中点,
∴EF为△ABC的中位线,
∴EF∥AC,EF=

AC,
∵F为AB中点,
∴AF=

AB,
∵AB=AC,
∴EF=AF,
又∵四边形ABED为平行四边形,
∴AF∥ME,
∵EF∥AC,
∴四边形AFEM为平行四边形,
∴四边形AFEM为菱形,∴②正确;
过F作FN⊥BC于N点,
则FN∥AE,
又∵F为AB的中点,
∴N为BE的中点,
∴FN为△ABE的中位线,
又∵AE=DC,BE=AD,
∴S
三角形BEF=

BE×FN=

×

CD×AD,S
三角形ACD=

AD×CD,
∴S
△BEF=

S
△ACD,∴③正确;
∵根据已知不能推出DE平分∠CDF,∴④错误;
故答案为:①②③.
点评:本题考查了三角形的中位线定理,矩形的性质和判定,菱形的判定,平行四边形的性质和判定,三角形的面积公式,线段的垂直平分线等知识点的综合运用,综合性比较强,有一定的难度.

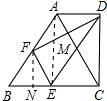
 如图,在梯形ABCD中,AD∥BC,∠BCD=90°,BC=2AD,F、E分别是BA、BC的中点,则下列结论正确的是________
如图,在梯形ABCD中,AD∥BC,∠BCD=90°,BC=2AD,F、E分别是BA、BC的中点,则下列结论正确的是________ S△ACD ④DE平分∠CDF.
S△ACD ④DE平分∠CDF.
 BC,
BC, AC,
AC, AB,
AB,
 BE×FN=
BE×FN= ×
× CD×AD,S三角形ACD=
CD×AD,S三角形ACD= AD×CD,
AD×CD, S△ACD,∴③正确;
S△ACD,∴③正确;

 如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )
如图,在梯形ABCD中,AD∥BC,∠BCD=90°,以CD为直径的半圆O切AB于点E,这个梯形的面积为21cm2,周长为20cm,那么半圆O的半径为( )