
【题目】如图,已知抛物线与x轴只有一个交点A(-2,0),与y轴交于点B(0,4).
(1)求抛物线对应的函数解析式;
(2)过点B做平行于x轴的直线交抛物线与点C.
①若点M在抛物线的AB段(不含A、B两点)上,求四边形BMAC面积最大时,点M的坐标;
②在平面直角坐标系内是否存在点P,使以P、A、B、C为顶点的四边形是平行四边形,若存在直接写出所有满足条件的点P的坐标;若不存在,请说明理由.
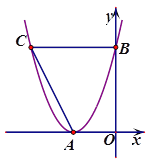
【答案】(1)y=(x+2)2 (2)①点M的坐标为(-1,1) ②存在 所有满足条件的点P的坐标是(2,0)、(-6,0)、(-2,8)
【解析】(1)由已知可设抛物线对应函数的解析式为:y=a(x+2)2(a≠0),∵抛物线与y轴交于点B(0,4)
∴4=a(0+2)2
解得:a=1
∴抛物线对应的解析式为:y=(x+2)2.
(2)①如图1中,设点M的坐标为(m,(m+2)2),其中﹣2<m<0,则N点坐标(m,0).
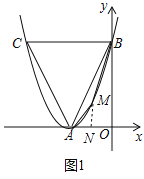
∵A、B、C是定点,∴若要四边形BMAC的面积最大,只要BMA的面积最大即可.
过M做MN⊥x轴于点N,则
S△AOB=![]() OAOB=
OAOB=![]() ×2×4=4
×2×4=4
S△AMN=![]() ANMN=
ANMN=![]() ×[m﹣(﹣2)]×(m+2)2=
×[m﹣(﹣2)]×(m+2)2=![]() (m+2)3
(m+2)3
S梯形ONMB=![]() ON(MN+OB)
ON(MN+OB)
=![]() ×(﹣m)×[(m+2)2+4]
×(﹣m)×[(m+2)2+4]
=﹣![]() (m3+4m2+8m)
(m3+4m2+8m)
∴S△AMB=S△AOB﹣S△AMN﹣S梯形ONMB
=4﹣![]() (m+2)3﹣[﹣
(m+2)3﹣[﹣![]() (m3+4m2+8m)]
(m3+4m2+8m)]
=﹣m2﹣2m,当m=﹣1时,S△AMB最大,∵(﹣1+2)2=1
∴此时点M的坐标为(﹣1,1).
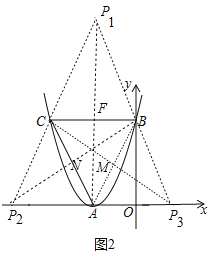
②存在.如图2中,∵四边形ABP1C是平行四边形,∴FC=FB,AF=FP1,∵B(0,4),C(﹣4,4),∴F(﹣2,4),设P1(x,y),则有![]() =﹣2,
=﹣2,![]() =4,∴x=﹣2,y=8,∴P1(﹣2,8),同法可得P2(﹣6,0),P3(2,0).
=4,∴x=﹣2,y=8,∴P1(﹣2,8),同法可得P2(﹣6,0),P3(2,0).
所有满足条件的点P的坐标是(2,0)、(﹣6,0)、(﹣2,8).


 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系xOy中,△ABC的三个顶点坐标分别为A(-4,1)、B(-1,1)、C(-4,3).
(1)画出Rt△ABC关于原点O成中心对称的图形Rt△A1B1C1;
(2)若Rt△ABC与Rt△A2BC2关于点B中心对称,则点A2的坐标为 、C2的坐标为 .
(3)求点A绕点B旋转180°到点A2时,点A在运动过程中经过的路程.

查看答案和解析>>
科目:初中数学 来源: 题型:
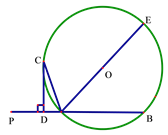
【题目】已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D
(1)求证:CD为⊙O的切线
(2)若DC+DA=6,⊙O的直径为10,求AB的长度。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里,装有三个分别标有数字1,2,3的小球,它们的形状、大小、质地等完全相同.小明先从盒子里随机取出一个小球,记下数字为x;放进盒子摇匀后,再由小华随机取出一个小球,记下数字为y.
(1)请用树状图或列表分析,写出(x,y)所有可能出现的结果;
(2)求小明、小华各取一次小球所确定的点(x,y)落在反比例函数![]() 图象上的概率.
图象上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com