


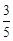 ,设AP=x,△PCE的面积为y,当AP>
,设AP=x,△PCE的面积为y,当AP>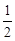 AC时,求y与x之间的函数关系式.
AC时,求y与x之间的函数关系式.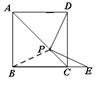
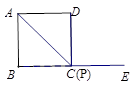
 ………………………..(4分)
………………………..(4分)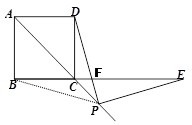
 ∴∠ABC=∠ADC=90°
∴∠ABC=∠ADC=90°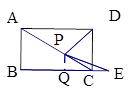
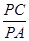 =
=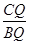
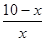 =
=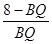
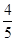 x, ∴BE=
x, ∴BE=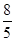 x, ∴CE=
x, ∴CE=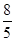 x-8
x-8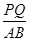 =
=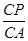 ∴
∴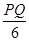 =
=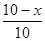
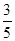 x
x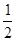 EC×PQ
EC×PQ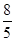 x-8)( 6-
x-8)( 6-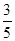 x)
x)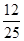 x2+
x2+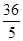 x-24(5<x<10) ……………………………..(7分)
x-24(5<x<10) ……………………………..(7分) 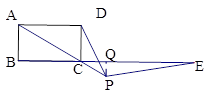
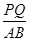 =
=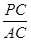
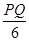 =
=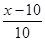
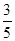 x-6
x-6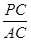 =
=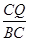
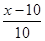 =
=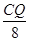
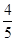 x-8
x-8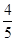 x
x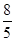 x
x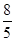 x-8
x-8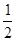 EC×PQ
EC×PQ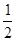 (
(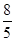 x-8) (
x-8) (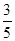 x-6)
x-6)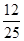
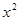 -
-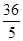 x+24(x>10) ………………………………………..(8分)
x+24(x>10) ………………………………………..(8分)

 53天天练系列答案
53天天练系列答案科目:初中数学 来源:不详 题型:填空题
 .(结果保留
.(结果保留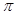 )
)
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
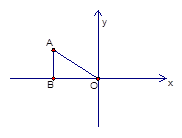
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.300 000km | B.30 000km | C.300km | D.30km |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
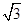 x和过x轴上的正奇数1、3、5、7、9、…所对应的点且与y轴平行的直线围成的.从左到右,将其面积依次记为S1、S2、S3、…、Sn、….则S1= ,Sn= .
x和过x轴上的正奇数1、3、5、7、9、…所对应的点且与y轴平行的直线围成的.从左到右,将其面积依次记为S1、S2、S3、…、Sn、….则S1= ,Sn= .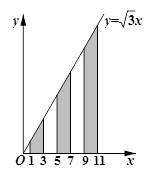
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com