
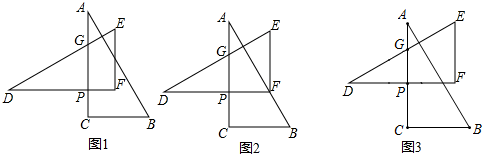
���� ��1������ֱ�������ε����ʣ��ɵ�AB�ij������ݹ��ɶ������ɵ�AC�ij���������ת�����ʣ��ɵ�DP�ij�����D�Ķ���������������Ǻ������ɵ�PG�ij��������߶εĺͲ�ɵô𰸣�
��2������ȫ�������ε��ж������ʣ��ɵ�PG��PF�Ĺ�ϵ��������ת�����ʣ��ɵ�PF��PC�Ĺ�ϵ�����ݵ����������ɵô𰸣�
��3�������߶��е�����ʣ��ɵ�DP�ij�������������Ǻ������ɵ�PG�ij��������߶εĺͲ�ɵ�AG�ij������ݱȵ����壬�ɵô𰸣�
��� �⣺��1���ɡ�C=90�㣬��A=30�㣬BC=$\sqrt{3}$����AB=2$\sqrt{3}$��
�ɹ��ɶ�������AC=3��
���߶εĺͲ��AP=AC-PC=3-t��
����ת�����ʣ���DP=AP=3-t����D=��A=30�㣬
PG=DP•tan��D=��3-t����$\frac{\sqrt{3}}{3}$=$\sqrt{3}$-$\frac{\sqrt{3}}{3}$t��
AG=AP-PG=��3-t��-��$\sqrt{3}$-$\frac{\sqrt{3}}{3}$t��=3-$\sqrt{3}$+��$\frac{\sqrt{3}}{3}$-1��t��
�ʴ�Ϊ��3-t��3-$\sqrt{3}$+��$\frac{\sqrt{3}}{3}$-1��t��
��2��֤�����ڡ�APF�͡�DPG�У�
$\left\{\begin{array}{l}{��A=��D}\\{AP=DP}\\{��APF=��DPG=90��}\end{array}\right.$��
���APF�ա�DPG��ASA����
��PF=PG��
���� P��תC��F���غϣ�
��PC=PF��
��PC=PG��
��3��DF=AC=3��
PΪDF���е㣬��DP=AP=$\frac{1}{2}$DF=$\frac{3}{2}$��
PG=DP•tan��D=$\frac{3}{2}$��tan30��=$\frac{3}{2}$��$\frac{\sqrt{3}}{3}$=$\frac{\sqrt{3}}{2}$��
���߶εĺͲ��
AG=AP-PG=$\frac{3}{2}$-$\frac{\sqrt{3}}{2}$��
$\frac{AG}{PG}$=$\frac{\frac{3-\sqrt{3}}{2}}{\frac{\sqrt{3}}{2}}$=$\sqrt{3}$-1��
���� ���⿼���˼��α任�ۺ��⣬��1����������ת�����ʣ�������Ǻ������߶εĺͲ��2��������ȫ�������ε��ж������ʣ���ת�����ʣ���3����������ת�����ʣ�������Ǻ������߶εĺͲ�ȵ����壮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����?ABCD�У�AD=3cm��AB=5cm��BD=4cm����?ABCD��������Խ���AC�ij���
��ͼ����?ABCD�У�AD=3cm��AB=5cm��BD=4cm����?ABCD��������Խ���AC�ij����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У���֪������AD��BF��CE�ཻ�ڵ�O�����1+��2+��3�Ķ�����
��ͼ���ڡ�ABC�У���֪������AD��BF��CE�ཻ�ڵ�O�����1+��2+��3�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ڡ�ABC�У���D�Ե�B���C�˶�����DE��AC��AB�ڵ�E����DF��AB��AC�ڵ�F��
��ͼ���ڡ�ABC�У���D�Ե�B���C�˶�����DE��AC��AB�ڵ�E����DF��AB��AC�ڵ�F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���� ˮλ | һ | �� | �� | �� | �� | �� | �� |
| ˮλ�仯/�� | +0.2 | +0.8 | -0.4 | +0.1 | +0.3 | -0.4 | -0.1 |
| ʵ��ˮλ/�� | 33.6 |

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com