
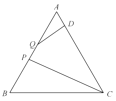
【题目】如图,等边![]() 的边长为3,点
的边长为3,点![]() 在边
在边![]() 上,
上,![]() ,线段
,线段![]() 在边
在边![]() 上运动,
上运动,![]() ,有下列结论:
,有下列结论:
①![]() 与
与![]() 可能相等;②
可能相等;②![]() 与
与![]() 可能相似;③四边形
可能相似;③四边形![]() 面积的最大值为
面积的最大值为![]() ;④四边形
;④四边形![]() 周长的最小值为
周长的最小值为![]() .其中,正确结论的序号为( )
.其中,正确结论的序号为( )
A.①④B.②④C.①③D.②③
【答案】D
【解析】
①通过分析图形,由线段![]() 在边
在边![]() 上运动,可得出
上运动,可得出![]() ,即可判断出
,即可判断出![]() 与
与![]() 不可能相等;
不可能相等;
②假设![]() 与
与![]() 相似,设
相似,设![]() ,利用相似三角形的性质得出
,利用相似三角形的性质得出![]() 的值,再与
的值,再与![]() 的取值范围进行比较,即可判断相似是否成立;
的取值范围进行比较,即可判断相似是否成立;
③过P作PE⊥BC于E,过F作DF⊥AB于F,利用函数求四边形![]() 面积的最大值,设
面积的最大值,设![]() ,可表示出
,可表示出![]() ,
,![]() ,可用函数表示出
,可用函数表示出![]() ,
,![]() ,再根据
,再根据![]() ,依据
,依据![]() ,即可得到四边形
,即可得到四边形![]() 面积的最大值;
面积的最大值;
④作点D关于直线![]() 的对称点D1,作D1D2∥PQ,连接CD2交AB于点P′,在射线P′A上取P′Q′=PQ,此时四边形P′CDQ′的周长为:
的对称点D1,作D1D2∥PQ,连接CD2交AB于点P′,在射线P′A上取P′Q′=PQ,此时四边形P′CDQ′的周长为:![]() ,其值最小,再由D1Q′=DQ′=D2 P′,
,其值最小,再由D1Q′=DQ′=D2 P′,![]() ,且∠AD1D2=120°,∠D2AC=90°,可得
,且∠AD1D2=120°,∠D2AC=90°,可得![]() 的最小值,即可得解.
的最小值,即可得解.
解:①∵线段![]() 在边
在边![]() 上运动,
上运动,![]() ,
,
∴![]() ,
,
∴![]() 与
与![]() 不可能相等,
不可能相等,
则①错误;
②设![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,即
,即![]() ,
,
假设![]() 与
与![]() 相似,
相似,
∵∠A=∠B=60°,
∴![]() ,即
,即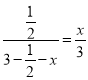 ,
,
从而得到![]() ,解得
,解得![]() 或
或![]() (经检验是原方程的根),
(经检验是原方程的根),
又![]() ,
,
∴解得的![]() 或
或![]() 符合题意,
符合题意,
即![]() 与
与![]() 可能相似,
可能相似,
则②正确;
③如图,过P作PE⊥BC于E,过D作DF⊥AB于F,
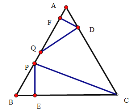
设![]() ,
,
由![]() ,
,![]() ,得
,得![]() ,即
,即![]() ,
,
∴![]() ,
,
∵∠B=60°,
∴![]() ,
,
∵![]() ,∠A =60°,
,∠A =60°,
∴![]() ,
,
则![]() ,
,
![]() ,
,
∴四边形![]() 面积为:
面积为:![]() ,
,
又∵![]() ,
,
∴当![]() 时,四边形
时,四边形![]() 面积最大,最大值为:
面积最大,最大值为:![]() ,
,
即四边形![]() 面积最大值为
面积最大值为![]() ,
,
则③正确;
④如图,作点D关于直线![]() 的对称点D1,作D1D2∥PQ,连接CD2交AB于点P′,在射线P′A上取P′Q′=PQ,
的对称点D1,作D1D2∥PQ,连接CD2交AB于点P′,在射线P′A上取P′Q′=PQ,
此时四边形P′CDQ′的周长为:![]() ,其值最小,
,其值最小,
∴D1Q′=DQ′=D2 P′,![]() ,
,
且∠AD1D2=180![]() ∠D1AB=180
∠D1AB=180![]() ∠DAB =120°,
∠DAB =120°,
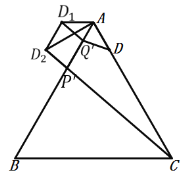
∴∠D1AD2=∠D2AD1=![]() =30°,∠D2AC=90°,
=30°,∠D2AC=90°,
在△D1AD2中,∠D1AD2=30°,![]() ,
,
∴![]() ,
,
在Rt△AD2C中,
由勾股定理可得,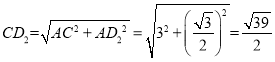 ,
,![]()
∴四边形P′CDQ′的周长为:
![]()
![]()
![]() ,
,
则④错误,
所以可得②③正确,
故选:D.


科目:初中数学 来源: 题型:
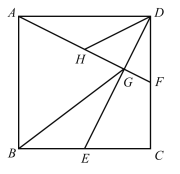
【题目】如图,在边长为4的正方形![]() 中,点
中,点![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,![]() 、
、![]() 交于点
交于点![]() ,
,![]() 的中点为
的中点为![]() ,连接
,连接![]() 、
、![]() .给出下列结论:①
.给出下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的结论有________.(请填上所有正确结论的序号)
.其中正确的结论有________.(请填上所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
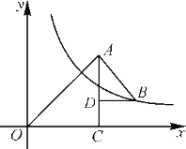
【题目】如图,△OAC和△BAD都是等腰直角三角形,![]() ,反比例函数
,反比例函数![]() 在第一象限的图象经过点B,则S△OAC-S△BAD=( )
在第一象限的图象经过点B,则S△OAC-S△BAD=( )
A.1.5B.2.5C.3D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节是中国的传统节日.今年端午节前夕,遂宁市某食品厂抽样调查了河东某居民区市民对A、B、C、D四种不同口味粽子样品的喜爱情况,并将调查情况绘制成如图两幅不完整统计图:
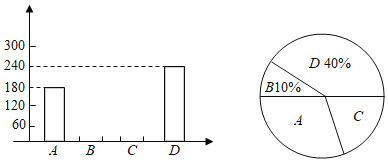
(1)本次参加抽样调查的居民有 人.
(2)喜欢C种口味粽子的人数所占圆心角为 度.根据题中信息补全条形统计图.
(3)若该居民小区有6000人,请你估计爱吃D种粽子的有 人.
(4)若有外型完全相同的A、B、C、D棕子各一个,煮熟后,小李吃了两个,请用列表或画树状图的方法求他第二个吃的粽子恰好是A种粽子的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校“校园主持人大赛”结束后,将所有参赛选手的比赛成绩(得分均为整数)进行整理,并分别绘制成扇形统计图和频数直方图.部分信息如下:
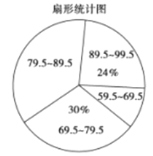
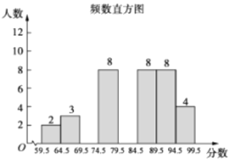
(1)本次比赛参赛选手共有________人,扇形统计图中“79.5~89.5”这一范围的人数占总参赛人数的百分比为________;
(2)补全图2频数直方图;
(3)赛前规定,成绩由高到低前40%的参赛选手获奖.某参赛选手的比赛成绩为88分,试判断他能否获奖,并说明理由;
(4)成绩前四名是2名男生和2名女生,若他们中任选2人作为该校文艺晚会的主持人,试求恰好选中1男1女为主持人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一块矩形地块![]() ,
,![]() 米,
米,![]() 米,为美观,拟种植不同的花卉,如图所示,将矩形
米,为美观,拟种植不同的花卉,如图所示,将矩形![]() 分割成四个等腰梯形及一个矩形,其中梯形的高相等,均为
分割成四个等腰梯形及一个矩形,其中梯形的高相等,均为![]() 米.现决定在等腰梯形
米.现决定在等腰梯形![]() 和
和![]() 中种植甲种花卉;在等腰梯形
中种植甲种花卉;在等腰梯形![]() 和
和![]() 中种植乙种花卉;在矩形
中种植乙种花卉;在矩形![]() 中种植丙种花卉.甲、乙、丙三种花卉的种植成本分别为20元/米
中种植丙种花卉.甲、乙、丙三种花卉的种植成本分别为20元/米![]() 、60 元/米
、60 元/米![]() 、40元/米
、40元/米![]() ,设三种花卉的种植总成本为
,设三种花卉的种植总成本为![]() 元.
元.
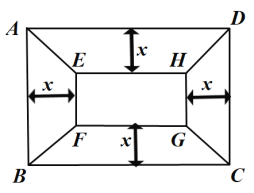
(1)当![]() 时,求种植总成本
时,求种植总成本![]() ;
;
(2)求种植总成本![]() 与
与![]() 的函数表达式,并写出自变量
的函数表达式,并写出自变量![]() 的取值范围;
的取值范围;
(3)若甲、乙两种花卉的种植面积之差不超过120米![]() ,求三种花卉的最低种植总成本.
,求三种花卉的最低种植总成本.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,P是对角线BD上的一点,过点C作CQ∥DB,且CQ=DP,连接AP、BQ、PQ.
(1)求证:△APD≌△BQC;
(2)若∠ABP+∠BQC=180°,求证:四边形ABQP为菱形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某小型汽车的侧面示意图,其中矩形ABCD表示该车的后备箱,在打开后备箱的过程中,箱盖ADE可以绕点A逆时针方向旋转,当旋转角是50度时,箱盖落在![]() 的位置(如图2),已知
的位置(如图2),已知![]()
![]()
![]()
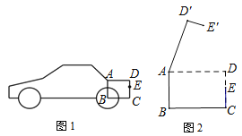
(1)求点![]() 到
到![]() 的距离;(结果保留整数)
的距离;(结果保留整数)
(2)求![]() 两点之间的距离.(结果保留整数)
两点之间的距离.(结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
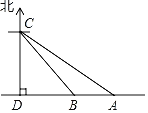
【题目】据调查:超速行驶是引发交通事故的主要原因之一.小明用所学知识对一条笔直公路上车辆进行测速,如图所示,观测点C到公路的距离CD=200m,检测路段的起点A位于点C的南偏东60°方向上,终点B位于点C的南偏东45°方向上,一辆轿车由东向西匀速行驶,测得此车由A处行驶到B处时的时间为10s,问此车是否超过了该路段10m/s的限制速度?(观测点C离地面的距离忽略不计,参专数据:![]() 1.41,
1.41,![]() 1.73)
1.73)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com