
【题目】在圆O中,弦AB与CD相交于点E,且弧AC与弧BD相等.点D在劣弧AB上,联结CO并延长交线段AB于点F,联结OA、OB.当OA=![]() ,且tan∠OAB=
,且tan∠OAB=![]() .
.
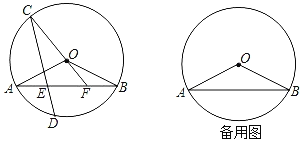
(1)求弦CD的长;
(2)如果△AOF是直角三角形,求线段EF的长;
(3)如果S△CEF=4S△BOF,求线段AF的长.
【答案】(1)4;(2)![]() 或
或![]() ;(3)2+
;(3)2+![]()
【解析】
(1)如图,过点O作OH⊥AB于点H,由锐角三角函数可求OH=1,AH=2,由垂径定理可得AB=4,即可求CD=4
(2)分两种情况讨论,由相似三角形的性质可求解;
(3)先利用面积关系得出![]() ,进而利用△OAF∽△EFC得出比例式,即可得出结论.
,进而利用△OAF∽△EFC得出比例式,即可得出结论.
解:(1)如图,过点O作OH⊥AB于点H,
∵tan∠OAB=![]() ,
,
∴设OH=a,AH=2a,
∵AO2=OH2+AH2=5,
∴a=1,
∴OH=1,AH=2,
∵OH⊥AB,
∴AB=2AH=4,
∵弧AC=弧BD
∴![]() ,
,
∴AB=CD=4;
(2)∵OA=OB,
∴∠OAF=∠OBA,
∴∠OAF=∠ECF,
①当∠AFO=90°时,
∵OA=![]() ,tan∠OBA=
,tan∠OBA=![]() ,
,
∴OC=OA=![]() ,OF=1,AB=4,
,OF=1,AB=4,
∴EF=CFtan∠ECF=CFtan∠OBA=![]() ;
;
②当∠AOF=90°时,
∵OA=OB,
∴∠OAF=∠OBA,
∴tan∠OAF=tan∠OBA=![]() ,
,
∵OA=![]() ,
,
∴OF=OAtan∠OAF=![]() ,
,
∴AF=![]() ,
,
∵∠OAF=∠OBA=∠ECF,∠OFA=∠EFC,
∴△OFA∽△EFC,
∴![]() ,
,
∴EF=![]() ,
,
即:EF=![]() 或
或![]() ;
;
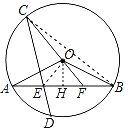
(3)如图,连接OE,
∵∠ECB=∠EBC,
∴CE=EB,
∵OE=OE,OB=OC,
∴△OEC≌△OEB,
∴S△OEC=S△OEB,
∵S△CEF=4S△BOF,
∴S△CEO+S△EOF=4(S△BOE﹣S△EOF),
∴![]() ,
,
∴![]() ,
,
∴FO=![]() ,
,
∵△OFA∽△EFC,
∴![]() ,
,
∴BF=BE﹣EF=CE﹣EF=![]() EF,
EF,
∴AF=AB﹣BF=4﹣![]() EF,
EF,
∵△OAF∽△EFC,
∴![]() ,
,
∴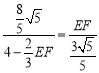 ,
,
∴EF=3﹣![]() ,
,
∴AF=4﹣![]() EF=2+
EF=2+![]() .
.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
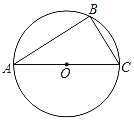
【题目】如图,已知⊙O为△ABC的外接圆,AC为直径,且AC=2![]() .
.
(1)用尺规作图作出∠ABE=45°,与弧AC交于E点(保留作图痕迹,不写作法);
(2)若∠A=30°,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
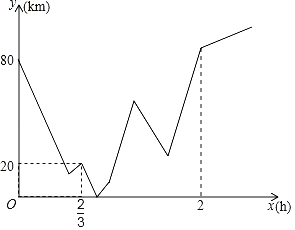
【题目】A、B两地之间有一修理厂C,一日小海和王陆分别从A、B两地同时出发相向而行,王陆开车,小海骑摩托.二人相遇时小海的摩托车突然出故障无法前行,王陆决定将小海和摩托车一起送回到修理厂C后再继续按原路前行,王陆到达A地后立即返回B地,到B地后不再继续前行,等待小海前来(装载摩托车时间和掉头时间忽略不计),整个行驶过程中王陆速度不变,而小海在修理厂花了十分钟修好摩托车,为了赶时间,提速![]() 前往目的地B,小海到达B地后也结束行程,若图象表示的是小海与王陆二人到修理厂C的距离和y(km)与小海出行时间之间x(h)的关系,则当王陆第二次与小海在行驶中相遇时,小海离目的地B还有_____km.
前往目的地B,小海到达B地后也结束行程,若图象表示的是小海与王陆二人到修理厂C的距离和y(km)与小海出行时间之间x(h)的关系,则当王陆第二次与小海在行驶中相遇时,小海离目的地B还有_____km.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019 年3月16日,由中国科协主办的第六届全国青年科普创新实验暨作品大赛启动,重点围绕“智能、环保、教育”三大主题,某中学派出甲、乙两组队伍参加本次大赛,有四个命题供他们选择:
①智能:智能控制及人工智能命题(用![]() 表示)
表示)
②环保:包括生物环境、风能两个命题(分别用![]() 表示)
表示)
③教育:未来教育命题(用![]() 表示)
表示)
![]() 甲组队伍在四个命题中随机选取一个报名 ,恰好选择“教育”主题的概率是多少?
甲组队伍在四个命题中随机选取一个报名 ,恰好选择“教育”主题的概率是多少?
![]() 若甲,乙两组队伍各随机从四个命题中选--个报名.请用树状图法或列表法求出他们都选择“环保”主题的概率.
若甲,乙两组队伍各随机从四个命题中选--个报名.请用树状图法或列表法求出他们都选择“环保”主题的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①在![]() 中,若点
中,若点![]() 在边
在边![]() 上,且
上,且![]() 则点
则点![]() 定义为
定义为![]() 的边
的边![]() 上的“金点”.
上的“金点”.
![]() 已知点
已知点![]() 是
是![]() 的边
的边![]() 上的“金点”:
上的“金点”:
①若![]() 则
则![]() 的长为 _;
的长为 _;
②若![]() 则
则![]() 的长为 _;
的长为 _;
![]() 在图①中,若点
在图①中,若点![]() 是
是![]() 的边
的边![]() 的中点,
的中点,![]() 试判断点
试判断点![]() 是不是
是不是![]() 的“金
的“金
点”,并说明理由;
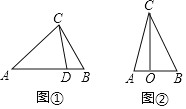
![]() 如图②,已知点
如图②,已知点![]() 为同一直线上三点,且
为同一直线上三点,且![]() 在
在![]() 所在直线上是否存在一点
所在直线上是否存在一点![]() 使点
使点![]() 中的某一点是其余三点围成的三角形的“金点”.若存在,求出线段
中的某一点是其余三点围成的三角形的“金点”.若存在,求出线段![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
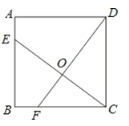
【题目】如图,已知正方形ABCD的边长为4,点E.F分别在边AB.BC上,且AE=BF=1,CE.DF交于点O.下列结论:①∠DOC=90°,②OC=OE,③tan∠OCD=![]() ,④S△ODC=S四边形BEOF中,正确的有_______________________.
,④S△ODC=S四边形BEOF中,正确的有_______________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
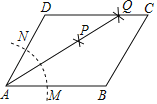
【题目】如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于![]() MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.
MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
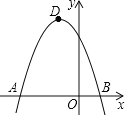
【题目】在平面直角坐标系中,二次函数y=-x2-bx+c的图象经过点A,点B(1,0)和点C(0,3).点D是抛物线的顶点.
(1)求二次函数的解析式和点D的坐标
(2)直线y=kx+n(k≠0)与抛物线交于点M,N,当△CMN的面积被y轴平分时,求k和n应满足的条件
(3)抛物线的对称轴与x轴交于点E,将抛物线向下平移m(m>0)个单位,平移后抛物线与y轴交于点C′,连接DC′,OD,是否存在OD平分∠C′DE的情况?若存在,求出m的值;若不荐在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
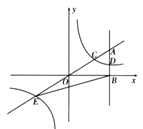
【题目】如图,在平面直角坐标系中,点A的坐标为![]() 轴于点
轴于点![]() ,反比例函数
,反比例函数![]() 的图像的一支分别交
的图像的一支分别交![]() 于点
于点![]() ,延长
,延长![]() 交反比例函数的图像的另一支于点E,已知D的纵坐标为
交反比例函数的图像的另一支于点E,已知D的纵坐标为![]() .
.
(1)求反比例函数的解析式及直线OA的解析式;
(2)连接BC,已知![]() ,求
,求![]()
(3)若在![]() 轴上有两点
轴上有两点![]() ,将直线
,将直线![]() 绕点
绕点![]() 旋转,仍与
旋转,仍与![]() 交于
交于![]() ,能否构成以
,能否构成以![]() 为顶点的四边形为菱形,如果能请求出
为顶点的四边形为菱形,如果能请求出![]() 的值,如果不能说明理由.
的值,如果不能说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com