
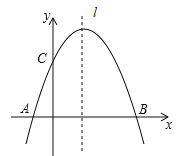
【题目】已知抛物线![]() 经过A(-1,0)、B(3,0)点,直线l是抛物线的对称轴.
经过A(-1,0)、B(3,0)点,直线l是抛物线的对称轴.
(1)求抛物线的函数关系式;
(2)在直线l上确定一点P,使△PAC的周长最小,求出点P的坐标.
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
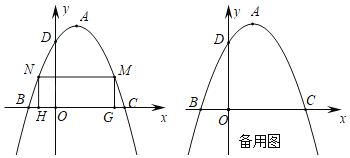
【题目】如图,已知二次函数图象的顶点坐标为![]() ,与坐标轴交于B、C、D三点,且B点的坐标为
,与坐标轴交于B、C、D三点,且B点的坐标为![]() .
.
(1)求二次函数的解析式;
(2)在二次函数图象位于x轴上方部分有两个动点M、N,且点N在点M的左侧,过M、N作x轴的垂线交x轴于点G、H两点,当四边形MNHG为矩形时,求该矩形周长的最大值;
(3)当矩形MNHG的周长最大时,能否在二次函数图象上找到一点P,使![]() 的面积是矩形MNHG面积的
的面积是矩形MNHG面积的![]() ?若存在,求出该点的横坐标;若不存在,请说明理由.
?若存在,求出该点的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3cm,BC=6cm.点P从点D出发向点A运动,运动到点A即停止;同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是1cm/s.连接PQ、AQ、CP.设点P、Q运动的时间为ts.
当t为何值时,四边形ABQP是矩形;
当t为何值时,四边形AQCP是菱形;
分别求出(2)中菱形AQCP的周长和面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
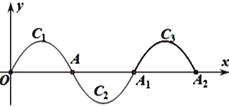
【题目】如图,一段抛物线:y=-x(x-2)(0≤x≤2)记为C1 ,它与x轴交于两点O,A;将C1绕点A旋转180°得到C2 , 交x轴于A1;将C2绕点A1旋转180°得到C3 , 交x轴于点A2 . .....如此进行下去,直至得到C2018 , 若点P(4035,m)在第2018段抛物线上,则m的值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区为了改善居住环境,准备修建一个巨型花园ABCD,为了节约材料并种植不同花卉,决定花园一边靠墙,三边用栅栏围住,中间用一段垂直于墙的栅栏隔成两块.已知所用栅栏的总长为60米,墙长为30米,设花园垂直于墙的一边的长为![]() 米.
米.

(1)若平行于墙的一边长为![]() 米,直接写出
米,直接写出![]() 与
与![]() 的函数关系式及自变量
的函数关系式及自变量![]() 的取值范围;
的取值范围;
(2)当![]() 为何值时,这个矩形花园的面积最大?最大值为多少?(栅栏占地面积忽略不计)
为何值时,这个矩形花园的面积最大?最大值为多少?(栅栏占地面积忽略不计)
(3)当这个花园的面积不小于288平方米时,试结合函数图象,直接写出![]() 的取值范围
的取值范围
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为实施国家“营养早餐”工程,食堂用甲、乙两种原料配制成某种营养食品,已知这两种原料的维生素C含量及购买这两种原料的价格如表:
原科维生素C及价格 | 甲种原料 | 乙种原料 |
维生素c(单位/千克) | 600 | 400 |
原料价格(元/千克) | 9 | 5 |
现要配制这种营养食品20千克,设购买甲种原料x千克,购买这两种原料的总费用为y元.
(1)求y与x的函数关系式?
(2)若食堂要求营养食品每千克至少含有480单位的维生素C,试说明需要购买甲种原料多少千克时,总费用最少?最少费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为决定谁获得仅有的一张电影票,甲和乙设计了如下游戏:在三张完全相同的卡片上,分别写上字母![]() ,
,![]() ,
,![]() ,背面朝上,每次活动洗均匀.
,背面朝上,每次活动洗均匀.
甲说:我随机抽取一张,若抽到字母![]() ,电影票归我;
,电影票归我;
乙说:我随机抽取一张后放回,再随机抽取一张,若两次抽取的字母相同的电影票归我.
![]() 求甲获得电影票的概率;
求甲获得电影票的概率;![]() 求乙获得电影票的概率;
求乙获得电影票的概率;![]() 此游戏对谁有利?
此游戏对谁有利?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com