
【题目】春节即将来临,某企业接到一批礼品生产任务,约定这批礼品的出厂价为每件6元,按要求在20天内完成.为了按时完成任务,该企业招收了新工人,设新工人小王第x天生产的礼品数量为y件,y与x满足如下关系:y=![]() .
.
(1)小王第几天生产的礼品数量为390件?
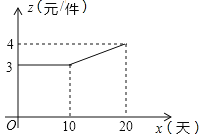
(2)如图,设第x天生产的每件礼品的成本是z元,z与x之间的关系可用图中的函数图象来刻画.若小王第x天创造的利润为w元,求w与x之间的函数表达式,并求出第几天的利润最大?最大利润是多少元?(利润=出厂价﹣成本)
【答案】(1)第12天生产的礼品数量为390只;(2)w与x的函数表达式为w=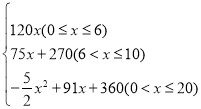 ,第18天利润最大,最大利润为1188元.
,第18天利润最大,最大利润为1188元.
【解析】
(1)因为前6天最多可生产礼品240只,所以把y=390代入y=25x+90,解方程即可求得;
(2)先根据图象求得成本z与x之间的关系,然后根据利润等于出厂价减去成本价,分0≤x≤6,6<x≤10,10<x≤20三种情况讨论,再根据一次函数的增减性和二次函数的增减性解答.
(1)∵6×40=240,
∴前六天中第6天生产的礼品最多达到240只,
将390代入y=25x+90得:25x+90=390,
∴x=12,
答:第12天生产的礼品数量为390只;
(2)当0≤x<10时,z=3,
当10≤x≤20时,设z=kx+b,将(10,3)和(20,4)代入,
得![]()
解得: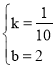 ,
,
∴z=![]() x+2;
x+2;
当0≤x≤6时,w=(6﹣3)×40x=120x,w随x的增大而增大,
∴当x=6时最大值为720元;
当6<x≤10时,w=(6﹣3)×(25x+90)=75x+270,w随x的增大而增大,
∴当x=10时最大值为1020元;
当10<x≤20时,w=(6﹣![]() x﹣2)(25x+90)=﹣
x﹣2)(25x+90)=﹣![]() x2+91x+360,
x2+91x+360,
∵对称轴为:直线x=18![]() ,天数为整数,
,天数为整数,
∴将x=18代入得w=1188元;
综上所述,w与x的函数表达式为w=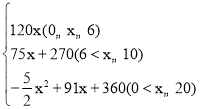 ,
,
答:第18天利润最大,最大利润为1188元.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:初中数学 来源: 题型:
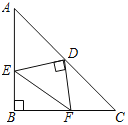
【题目】在等腰三角形ABC中,∠ABC=90°,D为AC边上中点,过D点作DE⊥DF,交AB于E,交BC于F,若AE=4,FC=3,则EF的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
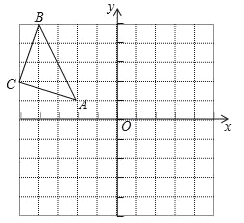
【题目】在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣4,5),C(﹣5,2).
(1)画出△ABC关于原点O成中心对称的△A1B1C1;
(2)写出△A1B1C1的顶点坐标;
(3)求出△A1B1C1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
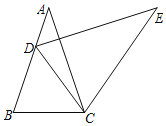
【题目】如图,△ABC中,AB=AC=2![]() ,tanB=3,点D为边AB上一动点,在直线DC上方作∠EDC=∠ECD=∠B,得到△EDC,则CE最小值为_____.
,tanB=3,点D为边AB上一动点,在直线DC上方作∠EDC=∠ECD=∠B,得到△EDC,则CE最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上学习了圆周角的概念和性质:“顶点在圆上,两边与圆相交”,“同弧所对的圆周角相等”,小明在课后继续对圆外角和圆内角进行了探究.
下面是他的探究过程,请补充完整:
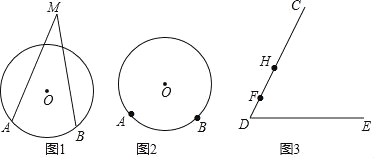
定义概念:顶点在圆外,两边与圆相交的角叫做圆外角,顶点在圆内,两边与圆相交的角叫做圆内角.如图1,∠M为![]() 所对的一个圆外角.
所对的一个圆外角.
(1)请在图2中画出![]() 所对的一个圆内角;
所对的一个圆内角;
提出猜想
(2)通过多次画图、测量,获得了两个猜想:一条弧所对的圆外角______这条弧所对的圆周角;一条弧所对的圆内角______这条弧所对的圆周角;(填“大于”、“等于”或“小于”)
推理证明:
(3)利用图1或图2,在以上两个猜想中任选一个进行证明;
问题解决
经过证明后,上述两个猜想都是正确的,继续探究发现,还可以解决下面的问题.
(4)如图3,F,H是∠CDE的边DC上两点,在边DE上找一点P使得∠FPH最大.请简述如何确定点P的位置.(写出思路即可,不要求写出作法和画图)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.

(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标:
(3)在抛物线上存在点P(不与C重合),使得△APB的面积与△ACB的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)求抛物线顶点M的坐标;
(2)设抛物线与x轴交于A、B两点,与y轴交于C点,求A、B、C的坐标(点A在点B的左侧),并画出函数图像的大致示意图;
(3)根据图像,写出不等式![]() 的解集.
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com