
分析 把抛物线化简成y=(k-1)(x-1)2+2-k,即可得出此抛物线的对称轴,当x=0和2时,y的值不受k是的影响,即可得出答案.
解答 解:∵抛物线y=(k-1)x2+(2-2k)x+1,
∴y=(k-1)(x2-2x)+1且k≠1,即y=(k-1)(x-1)2-(k-1)+1,且k≠1,
整理得:y=(k-1)(x-1)2+2-k且k≠1,
∴此抛物线的对称轴是x=1,
∵当x=0时,y=1,当x=2时,y=1,
∴此抛物线必定经过点(0,1)和点(2,1),
故答案为:x=1,(0,1)(2,1)
点评 本题主要考查了二次函数y=ax2+bx+c(a≠0)的对称轴直线是x=-$\frac{b}{2a}$,解答本题的关键就是把原抛物线化简成y=(k-1)(x-1)2+2+k且k≠1,然后再观察其图象.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:选择题
| A. | y=2x-14 | B. | y=-x-6 | C. | y=-x+10 | D. | y=4x |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
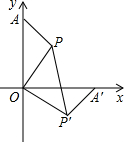 如图,在直角坐标系中,点A(0,5),点P(2,3),将△AOP绕点O顺时针方向旋转,使OA边落在x轴上,则点P'的坐标为(3,-2).
如图,在直角坐标系中,点A(0,5),点P(2,3),将△AOP绕点O顺时针方向旋转,使OA边落在x轴上,则点P'的坐标为(3,-2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | xy+2=1 | B. | x2+$\frac{1}{2x}$-9=0 | C. | ax2+bx+c=0 | D. | 2x2=3x-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知函数y=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$的图象与x轴交于点A,与y轴交于点B,点P是x轴上一点,若△PAB为等腰三角形,则点P的坐标不可能是( )
如图,已知函数y=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$的图象与x轴交于点A,与y轴交于点B,点P是x轴上一点,若△PAB为等腰三角形,则点P的坐标不可能是( )| A. | (-3-2$\sqrt{3}$,0) | B. | (3,0) | C. | (-1,0) | D. | (2$\sqrt{3}$,0) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com